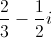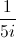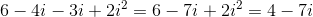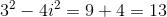Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Basic Operations with Complex Numbers

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #4681 : Algebra Ii

What is the absolute value of 4-3i $\displaystyle 4-3i$

Possible Answers:

$\frac{3}{4}$ $\displaystyle \frac{3}{4}$

$\displaystyle 5$

$\displaystyle -4$

$\frac{-4}{3}$ $\displaystyle \frac{-4}{3}$

$\displaystyle 3$

Correct answer:

$\displaystyle 5$

Explanation:

The absolute value is a measure of the distance of a point from the origin. Using the pythagorean distance formula to calculate this distance.

Report an Error

Example Question #1 : Basic Operations With Complex Numbers

Consider the following definitions of imaginary numbers:

$\displaystyle x = 4 - 2i$

$\displaystyle y = 6 +7i$

z = 5i $\displaystyle z = 5i$

Then, $\displaystyle x+y-2z = ?$

Possible Answers:

10-i $\displaystyle 10-i$

$\displaystyle 10$

2(5+i) $\displaystyle 2(5+i)$

-5i $\displaystyle -5i$

5(2-i) $\displaystyle 5(2-i)$

Correct answer:

5(2-i) $\displaystyle 5(2-i)$

Explanation:

$\displaystyle x + y-2z = (4-2i) + (6+7i) -2(5i) = 10 - 5i = 5(2-i)$

Report an Error

Example Question #4 : Imaginary Numbers

Simplify the expression.

$\displaystyle 4i^2-6i-7i^2+3i+4$

Possible Answers:

$\displaystyle -10$

-7-3i $\displaystyle -7-3i$

7-3i $\displaystyle 7-3i$

None of the other answer choices are correct.

$\displaystyle -3i^2-3i+4$

Correct answer:

7-3i $\displaystyle 7-3i$

Explanation:

Combine like terms. Treat $\small i$ $\displaystyle \small i$ as if it were any other variable.

$\displaystyle 4i^2-6i-7i^2+3i+4$

$\displaystyle -3i^2-3i+4$

Substitute to eliminate $\small i^2$ $\displaystyle \small i^2$ .

i^2=-1 $\displaystyle i^2=-1$

$\displaystyle -3(-1)-3i+4$

Simplify.

$\displaystyle 3-3i+4=7-3i$

Report an Error

Example Question #4684 : Algebra Ii

What is the value of $\displaystyle (3 + i)(4 + i)$ ?

Possible Answers:

$\displaystyle 4$

12 + 8i $\displaystyle 12 + 8i$

11 + 7i $\displaystyle 11 + 7i$

$\displaystyle 18$

12 + 6i $\displaystyle 12 + 6i$

Correct answer:

11 + 7i $\displaystyle 11 + 7i$

Explanation:

When dealing with imaginary numbers, we multiply by foiling as we do with binomials. When we do this we get the expression below:

$\displaystyle (3+i)(4+i)= 12 + 3i + 4i + i^2$

Since we know that $\displaystyle i^2 = -1$ we get $\displaystyle 12 + 7i - 1$ which gives us 11 + 7i $\displaystyle 11 + 7i$ .

Report an Error

Example Question #2 : Complex Numbers

What is the value of i^4 $\displaystyle i^4$ ?

Possible Answers:

$\displaystyle 3i$

$\displaystyle i$

$\displaystyle 1$

$\displaystyle -i$

i + 1 $\displaystyle i + 1$

Correct answer:

$\displaystyle 1$

Explanation:

Recall that the definition of imaginary numbers gives that $i = \sqrt{-1}$ $\displaystyle i = \sqrt{-1}$ and thus that $\displaystyle i^2 = -1$ . Therefore, we can use Exponent Rules to write $i^4 = i^2 \cdot i^2 = -1\cdot-1 = 1$ $\displaystyle i^4 = i^2 \cdot i^2 = -1\cdot-1 = 1$

Report an Error

Example Question #3 : Basic Operations With Complex Numbers

$\frac{1-7i}{6-2i}=a-i$ $\displaystyle \frac{1-7i}{6-2i}=a-i$

Find $\displaystyle a$ .

Possible Answers:

$\displaystyle 3$

$\displaystyle -4$

$\displaystyle 4$

0.5 $\displaystyle 0.5$

2.5 $\displaystyle 2.5$

Correct answer:

0.5 $\displaystyle 0.5$

Explanation:

Multiply the numerator and denominator by the numerator's complex conjugate.

$\frac{1-7i}{6-2i}\ast \frac{6+2i}{6+2i}=\frac{20-40i}{40}$ $\displaystyle \frac{1-7i}{6-2i}\ast \frac{6+2i}{6+2i}=\frac{20-40i}{40}$

Reduce/simplify.

Report an Error

Example Question #1 : How To Add Integers

Subtract:

$\displaystyle (-1+5i)-(2-3i)$

Possible Answers:

-3+8i $\displaystyle -3+8i$

-3+2i $\displaystyle -3+2i$

3-8i $\displaystyle 3-8i$

-3-8i $\displaystyle -3-8i$

-3-2i $\displaystyle -3-2i$

Correct answer:

-3+8i $\displaystyle -3+8i$

Explanation:

This is essentially the following expression after translation:

$\displaystyle (-1+5i)-(2-3i)=-1-2+5i+3i$

Now add the real parts together for a sum of $\displaystyle -3$ , and add the imaginary parts for a sum of $\displaystyle 8i$ .

Report an Error

Example Question #3 : Basic Operations With Complex Numbers

Multiply:

$\displaystyle (2+3i)(1-i)$

Answer must be in standard form.

Possible Answers:

2-3i $\displaystyle 2-3i$

5-i $\displaystyle 5-i$

5+i $\displaystyle 5+i$

2+2i $\displaystyle 2+2i$

$\displaystyle 5$

Correct answer:

5+i $\displaystyle 5+i$

Explanation:

$\displaystyle (2+3i)(1-i)$

The first step is to distribute which gives us:

$2-2i+3i-3i^{2}$ $\displaystyle 2-2i+3i-3i^{2}$

$2+i-3i^{2}=2+i+3=5+i$ $\displaystyle 2+i-3i^{2}=2+i+3=5+i$

which is in standard form.

Report an Error

Example Question #4681 : Algebra Ii

Add:

$\displaystyle (2-3i)+(-1-2i)$

Possible Answers:

5-3i $\displaystyle 5-3i$

1+5i $\displaystyle 1+5i$

5+3i $\displaystyle 5+3i$

1-5i $\displaystyle 1-5i$

-1+5i $\displaystyle -1+5i$

Correct answer:

1-5i $\displaystyle 1-5i$

Explanation:

When adding complex numbers, add the real parts and the imaginary parts separately to get another complex number in standard form.

Adding the real parts gives 2-1=1 $\displaystyle 2-1=1$ , and adding the imaginary parts gives -5i $\displaystyle -5i$ .

Report an Error

Example Question #4686 : Algebra Ii

Divide: $\frac{2-i}{3+2i}$ $\displaystyle \frac{2-i}{3+2i}$

The answer must be in standard form.

Possible Answers:

$\frac{2}{3}i$ $\displaystyle \frac{2}{3}i$

$\displaystyle i$

$\frac{1}{5i}$ $\displaystyle \frac{1}{5i}$

$\frac{2}{3}-\frac{1}{2}i$ $\displaystyle \frac{2}{3}-\frac{1}{2}i$

$\frac{4}{13}-\frac{7i}{13}$ $\displaystyle \frac{4}{13}-\frac{7i}{13}$

Correct answer:

$\frac{4}{13}-\frac{7i}{13}$ $\displaystyle \frac{4}{13}-\frac{7i}{13}$

Explanation:

Multiply both the numerator and the denominator by the conjugate of the denominator which is 3-2i $\displaystyle 3-2i$ which results in

$\frac{\left ( 2-i \right )\left ( 3-2i \right )}{\left ( 3+2i \right )\left ( 3-2i \right )}$ $\displaystyle \frac{\left ( 2-i \right )\left ( 3-2i \right )}{\left ( 3+2i \right )\left ( 3-2i \right )}$

The numerator after simplification give us $6-4i-3i+2i^{2}=6-7i+2i^{2}=4-7i$ $\displaystyle 6-4i-3i+2i^{2}=6-7i+2i^{2}=4-7i$

The denominator is equal to $3^{2}-4i^{2}=9+4=13$ $\displaystyle 3^{2}-4i^{2}=9+4=13$

Hence, the final answer in standard form =

$\frac{4}{13}-\frac{7i}{13}$ $\displaystyle \frac{4}{13}-\frac{7i}{13}$

Report an Error

View Algebra 2 Tutors

Sekou
Certified Tutor

University of New Haven, Bachelor in Arts, Mathematics.

View Algebra 2 Tutors

Akash
Certified Tutor

Georgia Institute of Technology-Main Campus, Bachelor of Engineering, Aerospace Engineering. Georgia Institute of Technology-...

View Algebra 2 Tutors

Therar
Certified Tutor

Beirut Arab University, Doctor of Philosophy, Mathematics. Saint Joseph University of Beirut, Master of Science, Counselor Ed...

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SAT Tutors in Dallas Fort Worth, Spanish Tutors in Chicago, ACT Tutors in Los Angeles, SSAT Tutors in Phoenix, Computer Science Tutors in Phoenix, Reading Tutors in Denver, Spanish Tutors in San Diego, MCAT Tutors in New York City, English Tutors in Philadelphia, English Tutors in Phoenix

Popular Courses & Classes

ACT Courses & Classes in Boston, GMAT Courses & Classes in New York City, GRE Courses & Classes in Houston, ACT Courses & Classes in Chicago, MCAT Courses & Classes in Philadelphia, SAT Courses & Classes in Phoenix, ACT Courses & Classes in San Diego, SAT Courses & Classes in Seattle, LSAT Courses & Classes in Chicago, GRE Courses & Classes in Philadelphia

Popular Test Prep

ISEE Test Prep in Washington DC, ACT Test Prep in Chicago, ISEE Test Prep in Chicago, SSAT Test Prep in Los Angeles, ACT Test Prep in Los Angeles, SAT Test Prep in Seattle, ACT Test Prep in Miami, SAT Test Prep in Atlanta, LSAT Test Prep in Boston, GRE Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Basic Operations with Complex Numbers

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #4681 : Algebra Ii

Example Question #1 : Basic Operations With Complex Numbers

Example Question #4 : Imaginary Numbers

Example Question #4684 : Algebra Ii

Example Question #2 : Complex Numbers

Example Question #3 : Basic Operations With Complex Numbers

Example Question #1 : How To Add Integers

Example Question #3 : Basic Operations With Complex Numbers

Example Question #4681 : Algebra Ii

Example Question #4686 : Algebra Ii

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: