Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Graphing Absolute Value Functions

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Graphing Absolute Value Functions

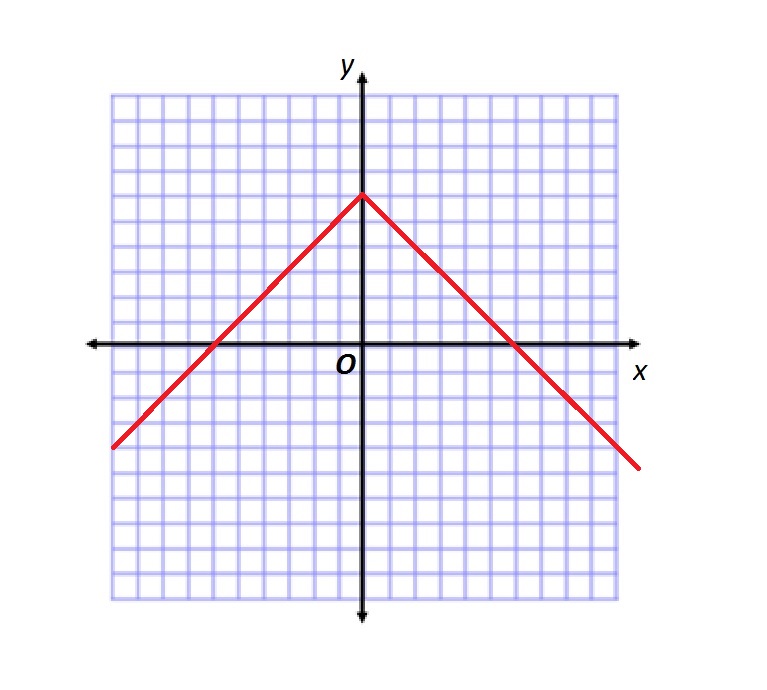
Axes_1

Refer to the above figure.

Which of the following functions is graphed?

Possible Answers:

g(x) = - |x| + 6

g(x) = |x| - 6

g(x) =- |x + 6|

g(x) = - |x|- 6

g(x) =- |x - 6|

Correct answer:

g(x) = - |x| + 6

Explanation:

Below is the graph of f(x) = |x| :

Axes_1

The given graph is the graph of reflected in the -axis, then translated up 6 units. This graph is

g (x) = -f(x ) + k , where k = 6 .

The function graphed is therefore

g (x) = -f(x ) + k

g (x) = -f(x ) + 6

g (x) = - |x|+ 6

Report an Error

Example Question #2 : Graphing Absolute Value Functions

Axes_1

Refer to the above figure.

Which of the following functions is graphed?

Possible Answers:

g(x) = - |x +2|

g(x) =2 - |x |

g(x) = -2 - |x |

g(x) = - |x -2|

g(x) = |x | -2

Correct answer:

g(x) = - |x +2|

Explanation:

Below is the graph of f(x) = |x| :

Axes_1

The given graph is the graph of reflected in the -axis, then translated left 2 units (or, equivalently, right units. This graph is

g (x) = -f(x-h) , where h = -2 .

The function graphed is therefore

g (x) = -f(x- (-2))

g (x) = -f(x+2)

g(x) = - |x +2|

Report an Error

Example Question #3 : Graphing Absolute Value Functions

Axes_1

Refer to the above figure.

Which of the following functions is graphed?

Possible Answers:

The correct answer is not given among the other responses.

g(x)= | x-7 | - 2

g(x)= | x-7 | + 2

g(x)= | x+7 | + 2

g(x)= | x+7 | - 2

Correct answer:

g(x)= | x+7 | - 2

Explanation:

Below is the graph of f(x) = |x| :

Axes_1

The given graph is the graph of translated by moving the graph 7 units left (that is, unit right) and 2 units down (that is, units up)

The function graphed is therefore

g (x) = f(x-h) + k where h = -7, k= -2 . That is,

g (x) = f(x-(-7)) + (-2)

g (x) = f(x+7) -2

g(x)= | x+7 | - 2

Report an Error

Example Question #3 : Graphing Absolute Value Functions

Screen_shot_2014-12-24_at_3.03.30_pm

What is the equation of the above function?

Possible Answers:

y=|2x+2|-3

y=|x+2|+3

$y=|\frac{x}{2}+2|-3$

y=|x+2|-3

y=|2(x+2)|-3

Correct answer:

y=|2(x+2)|-3

Explanation:

The formula of an absolute value function is y=|m(x-a)|+b where m is the slope, a is the horizontal shift and b is the vertical shift. The slope can be found with any two adjacent integer points, e.g. (0,1) and (1,3) , and plugging them into the slope formula, $m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$ , yielding m=2 . The vertical and horizontal shifts are determined by where the crux of the absolute value function is. In this case, at (-2,-3) , and those are your a and b, respectively.

Report an Error

Example Question #4 : Graphing Absolute Value Functions

Give the vertex of the graph of the function f(x) = |x + 6| - 7 .

Possible Answers:

(-6, -7)

(6, -7)

(-6, 7)

None of the other choices gives the correct response.

(6, 7)

Correct answer:

(-6, -7)

Explanation:

Let g(x) = |x|

The graph of this basic absolute value function is a "V"-shaped graph with a vertex at the origin, or the point with coordinates (0,0) . In terms of g(x) ,

f(x) = g(x + 6 )- 7

The graph of this function can be formed by shifting the graph of g(x) left 6 units ( ) and down 7 units (). The vertex is therefore located at (-6, -7) .

Report an Error

Example Question #2 : Graphing Absolute Value Functions

Give the vertex of the graph of the function f(x) = 10 - |x+ 10| .

Possible Answers:

(-10, 10)

(10, -10)

None of the other choices gives the correct response.

(10,10)

(-10, -10)

Correct answer:

(-10, 10)

Explanation:

Let g(x) = |x|

The graph of this basic absolute value function is a "V"-shaped graph with a vertex at the origin, or the point with coordinates (0,0) . In terms of g(x) ,

f(x) = 10 - g (x+ 10) ,

or, alternatively written,

f(x) = - g (x+ 10)+ 10

The graph of f(x) is the same as that of g(x) , after it shifts 10 units left ( g(x+10) ), it flips vertically (negative symbol), and it shifts up 10 units (the second +10 ). The flip does not affect the position of the vertex, but the shifts do; the vertex of the graph of f(x) is at (-10, 10) .

Report an Error

Example Question #7 : Graphing Absolute Value Functions

Which of the following absolute value functions is represented by the following graph?

Possible Answers:

$f(x)=2\left | x-3\right |+1$

$f(x)=3\left | x-3\right |+1$

$f(x)=2\left | x+3\right |+1$

$f(x)=3\left | x+3\right |+1$

The equation cannot be determined from the graph.

Correct answer:

$f(x)=2\left | x-3\right |+1$

Explanation:

The equation can be determined from the graph by following the rules of transformations; the base equation is:

$f(x)=\left | x\right |$

The graph of this base equation is:

When we compare our graph to the base equation graph, we see that it has been shifted right 3 units, up 1 unit, and our graph has been stretched vertically by a factor of 2. Following the rules of transformations, the equation for our graph is written as:

$f(x)=2\left | x-3\right |+1$

Report an Error

View Algebra 2 Tutors

Jonathan
Certified Tutor

University of Maryland-Baltimore County, Bachelor of Science, Mathematics.

View Algebra 2 Tutors

James
Certified Tutor

St. Mary of the Plains College, Bachelors, Mathematics. Baker University, Masters, Business Administration and Management.

View Algebra 2 Tutors

Anne
Certified Tutor

University of Maryland-Baltimore, Doctor of Science, Accounting.

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SAT Tutors in Los Angeles, Math Tutors in Miami, Physics Tutors in Miami, Statistics Tutors in Chicago, Math Tutors in New York City, Chemistry Tutors in Chicago, Physics Tutors in San Francisco-Bay Area, MCAT Tutors in Miami, MCAT Tutors in Atlanta, Algebra Tutors in Seattle

Popular Courses & Classes

ISEE Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Miami, MCAT Courses & Classes in Miami, ISEE Courses & Classes in Miami, SAT Courses & Classes in Philadelphia, LSAT Courses & Classes in New York City, GRE Courses & Classes in Boston, GMAT Courses & Classes in Boston, GMAT Courses & Classes in Seattle, ISEE Courses & Classes in San Diego

Popular Test Prep

SAT Test Prep in Denver, GRE Test Prep in New York City, GMAT Test Prep in Houston, ISEE Test Prep in Dallas Fort Worth, GRE Test Prep in Phoenix, ISEE Test Prep in Washington DC, ISEE Test Prep in San Diego, SSAT Test Prep in Miami, ISEE Test Prep in New York City, GRE Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Graphing Absolute Value Functions

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #1 : Graphing Absolute Value Functions

Example Question #2 : Graphing Absolute Value Functions

Example Question #3 : Graphing Absolute Value Functions

Example Question #3 : Graphing Absolute Value Functions

Example Question #4 : Graphing Absolute Value Functions

Example Question #2 : Graphing Absolute Value Functions

Example Question #7 : Graphing Absolute Value Functions

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: