All AP Calculus AB Resources
Example Questions
Example Question #47 : Integrals
If f(1) = 12, f' is continuous, and the integral from 1 to 4 of f'(x)dx = 16, what is the value of f(4)?
4
27
16
28
12
28
You are provided f(1) and are told to find the value of f(4). By the FTC, the following follows:
(integral from 1 to 4 of f'(x)dx) + f(1) = f(4)
16 + 12 = 28
Example Question #41 : Integrals
Find the limit.
lim as n approaches infiniti of ((4n3) – 6n)/((n3) – 2n2 + 6)
4
–6
0
1
nonexistent
4
lim as n approaches infiniti of ((4n3) – 6n)/((n3) – 2n2 + 6)
Use L'Hopitals rule to find the limit.
lim as n approaches infiniti of ((4n3) – 6n)/((n3) – 2n2 + 6)
lim as n approaches infiniti of ((12n2) – 6)/((3n2) – 4n + 6)
lim as n approaches infiniti of 24n/(6n – 4)
lim as n approaches infiniti of 24/6
The limit approaches 4.
Example Question #1 : Interpretations And Properties Of Definite Integrals
If a particle's movement is represented by 
The answer is 
now set 

Example Question #2 : Interpretations And Properties Of Definite Integrals
A particle's movement is represented by
At what time is the velocity at it's greatest?
The answer is at 6 seconds.

We can see that this equation will look like a upside down parabola so we know there will be only one maximum.
Now we set 

Example Question #3 : Interpretations And Properties Of Definite Integrals
What is the domain of 

Example Question #5 : Definite Integral Of The Rate Of Change Of A Quantity Over An Interval Interpreted As The Change Of The Quantity Over The Interval
If 
then at 

The answer is 8.
Example Question #51 : Integrals
Which of the following represents the graph of the polar function 
First, mulitply both sides by r.
Then, use the identities 

The answer is 
Example Question #4 : Interpretations And Properties Of Definite Integrals
What is the average value of the function 


The average function value is given by the following formula:
![Ave = \frac{1}{4} [x^{3}-\frac{5}{2}x^{2} + 7x]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/104059/gif.latex)


Example Question #5 : Interpretations And Properties Of Definite Integrals
If
then find 
We see the answer is 0 after we do the quotient rule.
Example Question #12 : Calculus 3
If 

According to the Fundamental Theorem of Calculus, if we take the derivative of the integral of a function, the result is the original function. This is because differentiation and integration are inverse operations.
For example, if 


We will apply the same principle to this problem. Because the integral is evaluated from 0 to 
The answer is 
All AP Calculus AB Resources













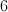



![(-\infty,-3]\cup [3,+\infty)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/27317/gif.latex)



































![Ave = \frac{1}{4}[(125-\frac{125}{2} + 35) - (1-\frac{5}{2}+7)] = 23](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/132675/gif.latex)




















