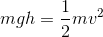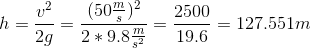Set the gravitational potential energy and kinetic energy equal to each other and solve for the height.

Mass cancels.

Isolate the height and plug in our values.

Rounding this gives .

To find terminal velocity, set the magnitude of the drag force equal to the magnitude of the force of gravity since when these forces are equal and opposite, the object will stop accelerating:

Solve for 

The ship's equation of velocity (found by solving the first-order differential equation) is 

Substitute  and solve.

Because the gravitational force depends only on the mass beneath the object (which is the gravitational version of Gauss's Law for charge), the acceleration steadily decreases as the object falls, and drops to zero at the center. Nevertheless, the velocity keeps increasing as the object falls, it just does so more slowly.

Relevant equations:

For the rocket to escape the moon's gravity, its minimum total energy is zero. If the total energy is zero, the rocket will have zero final velocity when it is infinitely far from the moon. If total energy is less than zero, the rocket will fall back to the moon's surface. If total energy is greater than zero, the rocket will have some final velocity when it is infinitely far away. 

For the minimum energy case as the rocket leaves the surface:

Rearrange energy equation to isolate the velocity term.

Substitute in the given values to solve for the velocity.

Relevant equations:

Use the given values to solve for the force.

Newton's law of universal gravitation states:

We can write two equations for the gravity experienced before and after the doubling:

The equation for gravity after the doubling can be simplified:

Because the masses of the spheres remain the same, as does the universal gravitation constant, we can substitute the definition of Fg1 into that equation:

The the gravitational force decreases by a factor of 4 when the distance between the two spheres is doubled.

Newton's law of universal gravitation states that:

We can write two equations representing the force of gravity before and after the doubling of the mass:

The problem gives us  and we can assume that all other variables stay constant.

Substituting these defintions into the second equation:

This equation simplifies to:

Substituting the definition of Fg1, we see:

Thus the gravitational forces doubles when the mass of one object doubles.

When the elevator accelerates upward, we know that an object would appear heavier. The normal force is the sum of all the forces added up, and in this case it is . We know that the normal force has two components, a component from gravity, and a component from the acceleration of the elevator. Using this equation, we can determine the mass of the block, which doesn't change:

 is acceleration due to gravity and  is the acceleration of the elevator.

When substituting in the values, we get 

Solving for , we get 

Since the elevator is descending at constant speed, no additional force is applied, therefore the force that the spring scale reads is only due to gravity, which is calculated by:

To do this problem we have to realize that the force of gravity acting on the bullet is equal to the centripetal force. The equations for gravitational force and centripetal force are as follows:

If we set the two equations equal to each other, the small  (mass of the bullet) will cancel out and  will disappear from the right side of the equation.

 is the universal gravitational constant 

 is given to be  and  to be .

If we plug everything in, we get

 or