All Calculus 3 Resources
Example Questions
Example Question #1 : Calculus 3
Suppose the vectors 


Example Question #2 : Calculus 3
The vector-valued function 


Find a tangent vector to 

Example Question #2 : Calculus 3
Let 
Find 
Example Question #4 : Calculus 3
Let 
Find its linear approximation at 
Hint: Use Taylor's formula.
Example Question #3 : Calculus 3
Let 

Notice that 




First, we need to find 

Then, we need to find 
The answer is 
Example Question #2 : Calculus 3
Evaluate:
cannot be determined
First, we can write out the first few terms of the sequence 

Notice that each term 







The answer is 
Example Question #4 : Calculus 3
Find 

We will have to find the first derivative of 




We will apply the chain rule on the left side.
We now solve for the first derivative with respect to 
In order to get the second derivative, we will differentiate 

We will replace 

But, from the original equation, 


The answer is 
Example Question #3 : Calculus 3
Which of the following represents the graph of the polar function 
First, mulitply both sides by r.
Then, use the identities 

The answer is 
Example Question #2 : Calculus 3
We can use the substitution technique to evaluate this integral.
Let 
We will differentiate 



We can solve for 


We will also need to change the bounds of the integral. When 



We will now substitute 



The answer is 
Example Question #5 : Calculus 3
Evaluate the following limit:
Does not exist.
First, let's multiply the numerator and denominator of the fraction in the limit by 
As 




The answer is 
Certified Tutor
Certified Tutor
All Calculus 3 Resources


























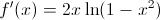






















![\frac{d}{dx}[y^2-x^2]=\frac{d}{dx}[4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/24767/gif.latex)
![\frac{d}{dx}[y^2]\cdot \frac{dy}{dx}-\frac{d}{dx}[x^2]=0](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/24768/gif.latex)


![\frac{d}{dx}\frac{dy}{dx}=\frac{d^{2}y}{dx^{2}}=\frac{d}{dx}[\frac{x}{y}]=\frac{y\cdot \frac{d}{dx}[x]-x\cdot \frac{d}{dx}[y]}{y^{2}} =\frac{y\cdot 1-x\cdot \frac{dy}{dx}}{y^{2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/24772/gif.latex)
































