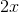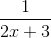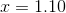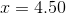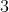To solve \(\displaystyle e^l^n^(^2^x^+^3^)\), it is necessary to know the property of \(\displaystyle e\).  

\(\displaystyle e^l^n^(^x^)=x\)

Since \(\displaystyle e\) and the \(\displaystyle ln\) terms cancel due to inverse operations, the answer is what's left of the \(\displaystyle ln\) term.

The answer is:  \(\displaystyle 2x+3\)

\(\displaystyle log{_{a}}^{b}=x\), \(\displaystyle b>0\)

\(\displaystyle \Rightarrow a^{x}=b\)

So, \(\displaystyle {{log_{4}}^{\frac{1}{2}}}=x\Rightarrow 4^{x}=\frac{1}{2}\)

This is a general formula that you should memorize. The inverse of \(\displaystyle Log_{b}x=y\) is \(\displaystyle b^{y}=x\). You can use this formula to change an equation from a log function to an exponential function.

Rewrite the following expression as an exponential expression:

\(\displaystyle log_3b=14,000\)

Recall the following property of logs and exponents:

\(\displaystyle log_b(a)=c\) 

Can be rewritten in the following form:

\(\displaystyle b^c=a\)

So, taking the log we are given;

\(\displaystyle log_3b=14,000\)

We can rewrite it in the form:

\(\displaystyle 3^{14,000}=b\)

So b must be a really huge number!

Convert the following logarithmic equation to an exponential equation:

\(\displaystyle log_{13}b=147\)

Recall the following:

This

\(\displaystyle log_b(a)=c\)

Can be rewritten as

\(\displaystyle b^c=a\)

So, our given logarithm

\(\displaystyle log_{13}b=147\)

Can be rewritten as

\(\displaystyle 13^{147}=b\)

Fortunately we don't need to expand, because this woud be a very large number!

Convert the following logarithmic equation to an exponential equation.

\(\displaystyle log_3(14x)=156\)

To convert from logarithms to exponents, recall the following property:

\(\displaystyle log_b(x)=a\)

Can be rewritten as:

\(\displaystyle b^a=x\)

So, starting with

\(\displaystyle log_3(14x)=156\),

We can get

\(\displaystyle 3^{156}=14x\)

To solve the following, you must "undo" the 5 with taking log based 5 of both sides. Thus,

\(\displaystyle 5^x=125\)

\(\displaystyle \log_5{5^x}=\log_5{125}\)

\(\displaystyle x=\log_5{125}\)

The right hand side can be simplified further, as 125 is a power of 5. Thus,

\(\displaystyle x=\log_5{125}\)

\(\displaystyle x=\log_5{5^3}\)

\(\displaystyle x=3\)

Apply the Product of Powers Property to rewrite the second expression:

\(\displaystyle 2^{x}+ 2 ^{x+2} = 171\)

\(\displaystyle 2^{x}+ 2 ^{2} \cdot 2 ^{x} = 171\)

\(\displaystyle 1 \cdot 2^{x}+ 4 \cdot 2 ^{x} = 171\)

Distribute out: 

\(\displaystyle (1 + 4) \cdot 2 ^{x} = 171\)

\(\displaystyle 5 \cdot 2 ^{x} = 171\)

Divide both sides by 5:

\(\displaystyle \frac{5 \cdot 2 ^{x}}{5} = \frac{171}{5}\)

\(\displaystyle 2 ^{x} = 34.2\)

Take the natural logarithm of both sides (and note that you can use common logarithms as well):

\(\displaystyle \ln 2 ^{x} = \ln 34.2\)

Apply a property of logarithms:

\(\displaystyle x \ln 2 = \ln 34.2\)

Divide by \(\displaystyle \ln 2\) and evaluate:

\(\displaystyle \frac{x \ln 2}{\ln2} = \frac{\ln 34.2}{\ln2}\)

\(\displaystyle x = \frac{3.5322 }{0.6931 }\)

\(\displaystyle x \approx 5.10\)

\(\displaystyle 9 = 3^{2}\), so rewrite the expression at right as a power of 3 using the Power of a Power Property:

\(\displaystyle 3^{2x+ 1} = 9^{2x- 4 }\)

\(\displaystyle 3^{2x+ 1} = (3^{2} )^{2x- 4 }\)

\(\displaystyle 3^{2x+ 1} = 3^{2(2x- 4 )}\)

Set the exponents equal to each other and solve the resulting linear equation:

\(\displaystyle 2x+ 1 = 2(2x-4)\)

Distribute:

\(\displaystyle 2x+ 1 = 4x-8\)

Subtract \(\displaystyle 4x\) and 1 from both sides; we can do this simultaneously:

\(\displaystyle 2x+ 1 - 4x - 1 = 4x-8 - 4x - 1\)

\(\displaystyle - 2x = -9\)

Divide by \(\displaystyle -2\):

\(\displaystyle \frac{- 2x}{-2} = \frac{-9}{-2}\)

\(\displaystyle x =4.5\)

To solve, you must first "undo" the log. Since no base is specified, you assume it is 10. Thus, we need to take 10 to both sides.

\(\displaystyle 10^{\log(2x+4)}=10^1\)

\(\displaystyle 2x+4=10\)

Now, simply solve for x.

\(\displaystyle 2x=6\)

\(\displaystyle x=3\)