GMAT Math : Calculating an angle in a quadrilateral

Study concepts, example questions & explanations for GMAT Math

Create An Account

All GMAT Math Resources

22 Diagnostic Tests 693 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Calculating An Angle In A Quadrilateral

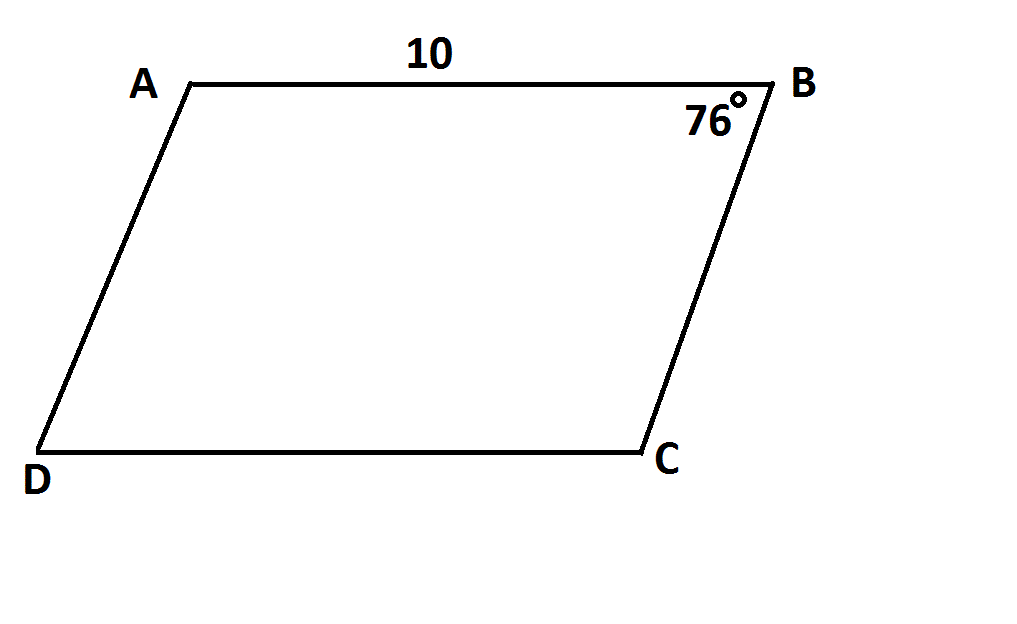
Parallelogram

Note: Diagram is NOT drawn to scale.

Refer to the above diagram.

Any of the following facts alone would be enough to prove that $\textrm{Quad} \; ABCD$ is not a parallelogram, EXCEPT:

Possible Answers:

Any one of these facts alone would prove that $\textrm{Quad} \; ABCD$ is not a parallelogram.

$m \angle A = 114^{\circ}$

BC > 12

$m \angle D <76^{\circ}$

CD = 12

Correct answer:

BC > 12

Explanation:

Opposite sides of a parallelogram are congruent; if CD = 12 , then $CD \neq AB$ , violating this condition.

Consecutive angles of a parallelogram are supplementary; if $m \angle A = 114^{\circ}$ , then $m \angle A + m \angle B= 114 + 76 = 190$ , violating this condition.

Opposite angles of a parallelogram are congruent; if $m \angle D <76^{\circ}$ , then $m \angle D \neq m \angle B$ , violating this condition.

Adjacent sides of a parallelogram, however, may or may not be congruent, so the condition that BC > 12 would not by itself prove that the quadrilateral is not a parallelogram.

Report an Error

Example Question #1 : Calculating An Angle In A Quadrilateral

Which of the following can not be the measures of the four interior angles of a quadrilateral?

Possible Answers:

All four of the other choices fit the conditions.

$80^{\circ },80^{\circ },100^{\circ },100^{\circ }$

$60^{\circ },100^{\circ },100^{\circ },100^{\circ }$

$75^{\circ },85^{\circ },95^{\circ },105^{\circ }$

$75^{\circ },75^{\circ },75^{\circ },125^{\circ }$

Correct answer:

$75^{\circ },75^{\circ },75^{\circ },125^{\circ }$

Explanation:

The four interior angles of a quadrilateral measure a total of $360^{\circ }$ , so we test each group of numbers to see if they have this sum.

75+85+95+105 = 360

80+80+100+100 = 360

60+100+100+100 = 360

75 + 75 + 75 + 125 = 350

This last group does not have the correct sum, so it is the correct choice.

Report an Error

Example Question #1 : Calculating An Angle In A Quadrilateral

A circle can be circumscribed about each of the following figures except:

Possible Answers:

A rectangle twice as long as it is wide

A rhombus with a $60^{\circ }$ angle

An isosceles trapezoid with one base three times as long as the other

A right scalene triangle

An isosceles triangle with its base one-half as long as either leg

Correct answer:

A rhombus with a $60^{\circ }$ angle

Explanation:

A circle can be circumscribed about any triangle regardless of its sidelengths or angle measures, so we can eliminate the two triangle choices.

A circle can be circumscribed about a quadrilateral if and only if both pairs of its opposite angles are supplementary. An isosceles trapezoid has this characteristic; this can be proved by the fact that base angles are congruent, and by the Same-Side Interior Angles Statement. For a parallelogram to have this characteristic, since opposite angles are congruent also, all angles must measure $90^{\circ }$ ; the rectangle fits this description, but the rhombus does not.

Report an Error

Example Question #3 : Calculating An Angle In A Quadrilateral

Rhombus RHOM has two diagonals that intersect at point ; $\angle RHO = 80 ^{\circ }$ .

What is $m \angle RPH$ ?

Possible Answers:

$40 ^{\circ }$

$90 ^{\circ }$

$80 ^{\circ }$

$100 ^{\circ }$

$50 ^{\circ }$

Correct answer:

$90 ^{\circ }$

Explanation:

The diagonals of a rhombus always intersect at right angles, so $m \angle HPO = 90 ^{\circ }$ . The measures of the interior angles of the rhombus are irrelevant.

Report an Error

Example Question #241 : Geometry

Quadrilateral QUAD is inscribed in circle $\bigodot$ . $m \angle A = 100 ^{\circ }$ . What is $m \angle Q$ ?

Possible Answers:

$40^{\circ }$

$160 ^{\circ }$

$100 ^{\circ }$

$50 ^{\circ }$

$80 ^{\circ }$

Correct answer:

$80 ^{\circ }$

Explanation:

Two opposite angles of a quadrilateral inscribed inside a circle are supplementary, so

$m \angle Q = 180^{\circ } - m \angle A = 180^{\circ } - 100^{\circ } = 80^{\circ }$

Report an Error

Example Question #41 : Other Quadrilaterals

Rhombus

Note: Figure NOT drawn to scale.

The above figure is of a rhombus and one of its diagonals. What is equal to?

Possible Answers:

x = 114

x = 138

x = 156

x = 132

Not enough information is given to answer the question.

Correct answer:

x = 132

Explanation:

The four sides of a rhombus are congruent, so a diagonal of the rhombus cuts it into two isosceles triangles. The two angles adjacent to the diagonal are congruent, so the third angle, the one marked, measures:

$\left (180 - 2 \times 24 \right )^{\circ } = \left (180 -48 \right )^{\circ } = 132^{\circ }$

Report an Error

Example Question #1 : Calculating An Angle In A Quadrilateral

Rectangle

Refer to the above figure. You are given that Polygon ABCD is a parallelogram, but NOT that it is a rectangle.

Which of the following statements is not enough to prove that Polygon ABCD is also a rectangle?

Possible Answers:

$\overline{BC} \perp \overline{DC}$

$m \angle 1 = 90^{\circ }$

$\angle BAC \cong \angle ACD$

$\angle BAC$ and $\angle CAD$ are complementary angles

$(AD)^{2} + (DC)^{2} = (AC)^{2}$

Correct answer:

$\angle BAC \cong \angle ACD$

Explanation:

To prove that Polygon ABCD is also a rectangle, we need to prove that any one of its angles is a right angle.

If $\overline{BC} \perp \overline{DC}$ , then by definition of perpendicular lines, $\angle BCD$ is right.

If $m \angle 1 = 90^{\circ }$ , then, since $\angle 1$ and $\angle BCD$ form a linear pair, $\angle BCD$ is right.

If $(AD)^{2} + (DC)^{2} = (AC)^{2}$ , then, by the Converse of the Pythagorean Theorem, $\Delta ADC$ is a right triangle with right angle $\angle D$ .

If $\angle BAC$ and $\angle CAD$ are complementary angles, then, since $m \angle BAC + m \angle CAD =m \angle BA D$

$m \angle BAD = m \angle BAC + m \angle CAD = 90 ^{\circ }$ , making $m \angle BAD$ right.

However, since, by definition of a parallelogram, $\overline{AB } \parallel \overline{ CD }$ , by the Alternate Interior Angles Theorem, $\angle BAC \cong \angle ACD$ regardless of whether the parallelogram is a rectangle or not.

Report an Error

Example Question #2 : Calculating An Angle In A Quadrilateral

Two angles of a parallelogram measure $\left ( x + 70 \right )^{\circ }$ and $\left ( 2x\right +5) ^{\circ }$ . What are the possible values of ?

Possible Answers:

$x = 35 \textrm{ or } x = 95$

x = 35

$x = 35 \textrm{ or } x = 65$

x = 65

x = 95

Correct answer:

$x = 35 \textrm{ or } x = 65$

Explanation:

Case 1: The two angles are opposite angles of the parallelogram. In this case, they are congruent, and

2x +5 = x + 70

2x +5 - x - 5 = x + 70 - x - 5

x = 65

Case 2: The two angles are consecutive angles of the parallelogram. In this case, they are supplementary, and

$\left ( 2x +5 \right )+\left ( x + 70 \right ) = 180$

3x+ 75 = 180

3x+ 75 -75 = 180 -75

3x = 105

$3x \div 3 = 105\div 3$

x = 35

Report an Error

All GMAT Math Resources

22 Diagnostic Tests 693 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Statistics Tutors in Atlanta, SSAT Tutors in New York City, Math Tutors in San Diego, Spanish Tutors in Miami, SSAT Tutors in Los Angeles, Chemistry Tutors in New York City, Biology Tutors in Dallas Fort Worth, French Tutors in Dallas Fort Worth, ISEE Tutors in Dallas Fort Worth, English Tutors in Los Angeles

Popular Courses & Classes

GMAT Courses & Classes in San Francisco-Bay Area, MCAT Courses & Classes in Washington DC, ACT Courses & Classes in Denver, LSAT Courses & Classes in Los Angeles, MCAT Courses & Classes in Miami, GMAT Courses & Classes in Chicago, LSAT Courses & Classes in Denver, SSAT Courses & Classes in Denver, SAT Courses & Classes in Los Angeles, GMAT Courses & Classes in San Diego

Popular Test Prep

GMAT Test Prep in San Francisco-Bay Area, LSAT Test Prep in San Diego, SAT Test Prep in New York City, GMAT Test Prep in Los Angeles, SAT Test Prep in San Diego, ISEE Test Prep in Houston, ISEE Test Prep in Los Angeles, GMAT Test Prep in Chicago, ACT Test Prep in Denver, SAT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

Email address:
Your name:
Feedback:

GMAT Math : Calculating an angle in a quadrilateral

Study concepts, example questions & explanations for GMAT Math

All GMAT Math Resources

Example Questions

Example Question #1 : Calculating An Angle In A Quadrilateral

Example Question #1 : Calculating An Angle In A Quadrilateral

Example Question #1 : Calculating An Angle In A Quadrilateral

Example Question #3 : Calculating An Angle In A Quadrilateral

Example Question #241 : Geometry

Example Question #41 : Other Quadrilaterals

Example Question #1 : Calculating An Angle In A Quadrilateral

Example Question #2 : Calculating An Angle In A Quadrilateral

All GMAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details