All Intermediate Geometry Resources
Example Questions
Example Question #44 : Pentagons
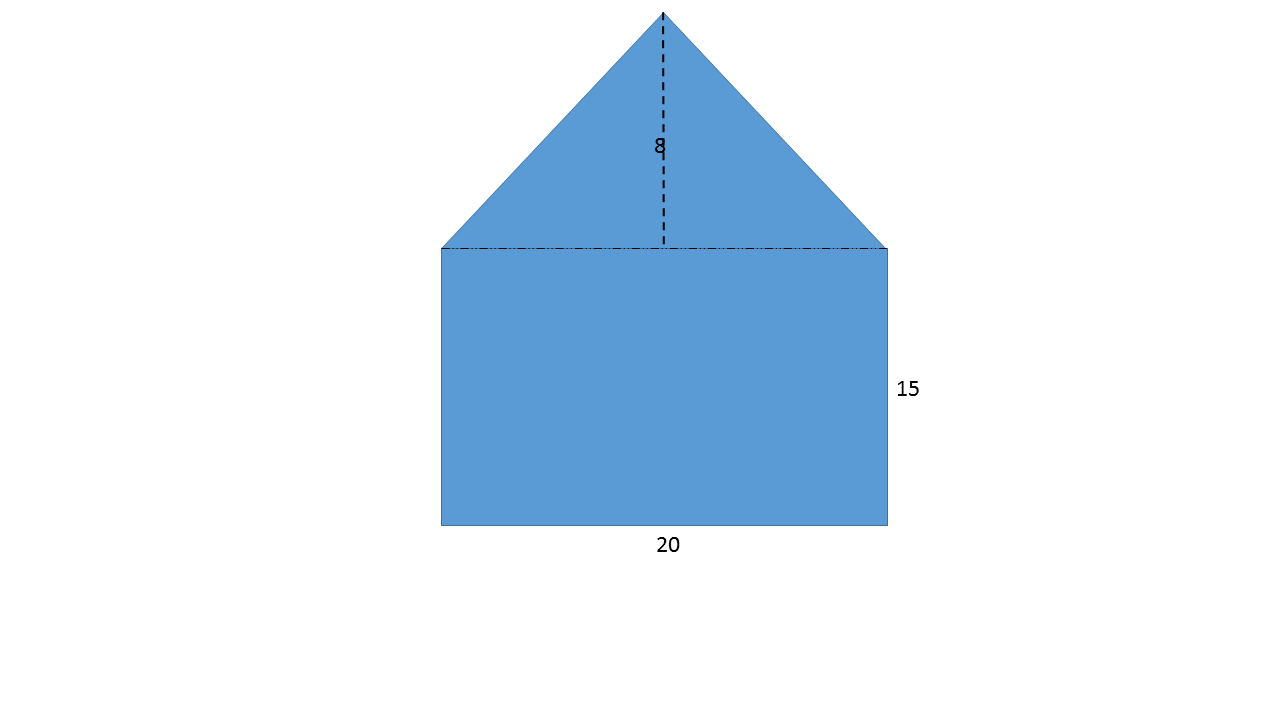
Find the area of the pentagon shown above.






To find the area of this pentagon, divide the interior of the pentagon into a four-sided rectangle and two right triangles. The area of the bottom rectangle can be found using the formula:
The area of the two right triangles can be found using the formula:
Since there are two right triangles, the sum of both will equal the area of the entire triangular top portion of the pentagon.
Thus, the solution is:
Example Question #1 : How To Find The Area Of A Pentagon

Find the area of the pentagon shown above.





To find the area of this pentagon, divide the interior of the pentagon into a four-sided rectangle and two right triangles. The area of the bottom rectangle can be found using the formula:
The area of the two right triangles can be found using the formula:
Since there are two right triangles, the sum of both will equal the area of the entire triangular top portion of the pentagon.
Thus, the solution is:
Example Question #1 : How To Find The Area Of A Pentagon
A regular pentagon has a side length of 






By definition a regular pentagon must have 






The area of this pentagon can be found by applying the area of a triangle formula: 
Note: the area shown above is only the a measurement from one of the five total interior triangles. Thus, to find the total area of the pentagon multiply: 
Example Question #46 : Pentagons
A regular pentagon has a side length of 







By definition a regular pentagon must have 

This question provides the length of the apothem of the pentagon--which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into 


The area of this pentagon can be found by applying the area of a triangle formula:
Note: 
Example Question #1 : How To Find The Area Of A Pentagon
A regular pentagon has a perimeter of 







To solve this problem, first work backwards using the perimeter formula for a regular pentagon:
Now you have enough information to find the area of this regular triangle.
Note: a regular pentagon must have 

This question provides the length of the apothem of the pentagon—which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into 


The area of this pentagon can be found by applying the area of a triangle formula:
Thus, the area of the entire pentagon is:
Example Question #47 : Pentagons
A regular pentagon has a side length of 







By definition a regular pentagon must have 

This question provides the length of the apothem of the pentagon—which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into 


The area of this pentagon can be found by applying the area of a triangle formula:
Keep in mind that this is the area for only one of the five total interior triangles.
The total area of the pentagon is:
Example Question #7 : How To Find The Area Of A Pentagon
A regular pentagon has a perimeter of 






To solve this problem, first work backwards using the perimeter formula for a regular pentagon:
Now you have enough information to find the area of this regular triangle.
Note: a regular pentagon must have 

This question provides the length of the apothem of the pentagon—which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into 


The area of this pentagon can be found by applying the area of a triangle formula:
To find the total area of the pentagon multiply:
Example Question #1 : How To Find The Area Of A Pentagon
A regular pentagon has a side length of 







By definition a regular pentagon must have 

This question provides the length of the apothem of the pentagon—which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into 


The area of this pentagon can be found by applying the area of a triangle formula:
However, the total area of the pentagon is equal to:
Example Question #2 : How To Find The Area Of A Pentagon
A regular pentagon has a side length of 






By definition a regular pentagon must have 

This question provides the length of the apothem of the pentagon—which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into 


The area of this pentagon can be found by applying the area of a triangle formula:
Note: 
Example Question #3 : How To Find The Area Of A Pentagon
A regular pentagon has a perimeter of 

To solve this problem, first work backwards using the perimeter formula for a regular pentagon:
Now you have enough information to find the area of this regular triangle.
Note: a regular pentagon must have 

This question provides the length of the apothem of the pentagon—which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into 


The area of this pentagon can be found by applying the area of a triangle formula:
Thus, the area of the entire pentagon is:
All Intermediate Geometry Resources















































