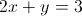is given in the slope-intercept form.  So the slope is  and the y-intercept is .

If the lines are perpendicular, then so the new slope must be

Next we substitute the new slope and the given point into the slope-intercept form of the equation to calculate the intercept.  So the equation to solve becomes so

So the equation of the perpendicular line becomes or in standard form

The definition of a perpendicular line is one that has a negative, reciprocal slope to another.

For this particular problem, we must first manipulate our initial equation into a more easily recognizable and useful form: slope-intercept form or .

According to our  formula, our slope for the original line is . We are looking for an answer that has a perpendicular slope, or an opposite reciprocal. The opposite reciprocal of  is . Flip the original and multiply it by . 

Our answer will have a slope of . Search the answer choices for  in the  position of the equation.

is our answer. 

(As an aside, the negative reciprocal of 4 is . Place the whole number over one and then flip/negate. This does not apply to the above problem, but should be understood to tackle certain permutations of this problem type where the original slope is an integer.)

The definition of a perpendicular line is a line with a negative reciprocal slope and identical intercept.

Therefore we need a line with slope 3 and intercept 2.

This means the only fitting line is .

To find the perpendicular line to

we need to find the negative reciprocal of the slope of the above equation.

So the slope of the above equation is  since  changes by  when  is incremented.

The negative reciprocal is:

So we are looking for an equation with a .

Only  satisfies this condition.

Determine the slope of the function .  The slope is: 

The slope of a perpendicular line is the negative reciprocal of the original slope. Determine the value of the slope perpendicular to the original function.

Plug in the given point and the slope to the slope-intercept form to find the y-intercept.

Substitute the slope of the perpendicular line and the new y-intercept back in the slope-intercept equation, .

The correct answer is:  

Find the slope from the given equation . The slope is: .

The slope of the perpendicular line is the negative reciprocal of the original slope.

Plug in the perpendicular slope and the given point to the slope-intercept equation.

Plug in the perpendicular slope and the y-intercept into the slope-intercept equation to get the equation of the perpendicular line.

Since we need a line perpendicular to    we know our slope must be  . This is because perpendicular lines have slopes that are negative reciprocals of each other. In order for our new line to pass through the point  we must use the point slope formula. Be sure to use the perpendicular slope.

A line perpendicular to another line will have as its slope the opposite of the reciprocal of the slope of the latter. Therefore, it is necessary to find the slope of the line of the equation 

Rewrite the equation in slope-intercept form . , the coefficient of , will be the slope of the line.

Add  to both sides:

Multiply both sides by , distributing on the right:

The slope of this line is . The slope of the first line will be the opposite of the reciprocal of this, or . The slope-intercept form of the equation of this line will be 

.

To find , set  and  and solve:

Add  to both sides:

The equation, in slope-intercept form, is .

To rewrite in standard form with integer coefficients:

Multiply both sides by 5:

Add  to both sides:

or