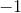All Intermediate Geometry Resources
Example Questions
Example Question #151 : Lines
Any line that is perpendicular to 
Two lines are perpendicular if and only if their slopes are negative reciprocals of each other. To find the slope, we must put the equation into slope-intercept form, 







Example Question #1 : How To Find The Slope Of A Perpendicular Line
What is the slope of any line perpendicular to 
The slope of a perpendicular line is the negative reciprocal of the original slope.
The original slope is 
The negative reciprocal of the original slope is:
Example Question #11 : Perpendicular Lines
What is the slope of a line perpendicular to 
The equation 
The correct answer is 
Example Question #1 : How To Find The Slope Of A Perpendicular Line
Assume the points 

Write the slope formula and find the slope of the first line.
The slope of the perpendicular line is the negative reciprocal of the original slope.
Therefore, the slope of the perpendicular line is 
Example Question #1442 : Intermediate Geometry
A line goes through the following 

Find the slope of a line perpendicular to the line given.
The slope of a line perpendicular is the negative reciprocal of the given line.
Since the given slope is calculated as 

Certified Tutor
Certified Tutor
All Intermediate Geometry Resources