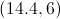All Intermediate Geometry Resources
Example Questions
Example Question #1 : How To Find Out If A Point Is On A Line With An Equation
A line passes through both the origin and the point 
Because the line passes through the origin, all of the points on the line will have an 


Example Question #71 : Lines
Which of the following points does NOT lie on the graph of
To find if a point lies on a graph or not, simply plug the x and y values into your equation and see if it holds true. Plugging our x values into the equation 

So our points are 


Example Question #3 : How To Find Out If A Point Is On A Line With An Equation
Which of the following points exists on the line 
Substitute each answer choice into the equation in question, 
Only 
Example Question #1 : Other Lines
Which of the following points exist on the line 
The line 


The only possible point with an 


Example Question #5 : How To Find Out If A Point Is On A Line With An Equation
Which point will exist on the line 
The line 


The only possible answer with a 


Example Question #1 : Other Lines
Which point is on the line 
A point is on a line if, plugged in, it creates a true mathematical equation.
For example, 





The point that does not work is 


Since this is not true, the point is NOT on the line.
Example Question #2 : Other Lines
Which point is NOT on the line 
A point is on a line if, plugged in, it creates a true mathematical equation.
For example, 





The point that does not work is 


Since this is not true, the point is NOT on the line.
Example Question #3 : Other Lines
Which point is NOT on the line 
A point is on a line if, plugged in, it creates a true mathematical equation.
For example, 





The point that does not work is 


Since this is not true, the point is NOT on the line.
Example Question #9 : How To Find Out If A Point Is On A Line With An Equation
Which point is NOT on the line 
A point is on a line if, plugged in, it creates a true mathematical equation.
For example, 





The point that does not work is 


Since this is not true, the point is NOT on the line.
Example Question #10 : How To Find Out If A Point Is On A Line With An Equation
The equation of a line is given below:
which point below can be found is NOT on the line?
To find the solution to this problem just do a quick check, pluggin in each point's x and y value into the equation. Remember coordinates are written with the x-value first, then the y-value (x,y).
If you try each point the only one that doesn't work is (8,2) !
In other words, if the x-value is 8 the y-value should be 4!
All Intermediate Geometry Resources