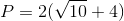Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Lower Level Quantitative : Coordinate Geometry

Study concepts, example questions & explanations for ISEE Lower Level Quantitative

Create An Account

All ISEE Lower Level Quantitative Resources

20 Diagnostic Tests 114 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Coordinate Geometry

New_vt_custom_xy_plane5

The parallelogram shown above has a height of and a base of length . Find the area of the parallelogram.

Possible Answers:

square units

Correct answer:

square units

Explanation:

To find the area of the parallelogram apply the formula: $A=base\times height$

Since, the paralleogram has a base of and a height of the solution is:
$A=5\times4=20$

Report an Error

Example Question #2 : Coordinate Geometry

New_vt_custom_xy_plane5

The parallelogram shown above has a height of and a base of length . Find the perimeter of the parallelogram.

Possible Answers:

$P=(\sqrt{20}+5)$

p=2(20+5)

$P=2(\sqrt{20}+5)$

$P=2(\sqrt{20}+4)$

Correct answer:

$P=2(\sqrt{20}+5)$

Explanation:

In order to find the correct perimeter of the parallelogram apply the formula: P=2(a+b) , where the length of one of the diagonal sides and the length of the base.

In order to find the length of side , apply the formula: a^2+b^2=C^2 . By drawing an altitude from point (4,4) to (4,0) , a right triangle is formed with a base that has a length of and a height of .

Thus, the solution is:
a^2 +b^2=c^2
2^2+4^2= length of side a^2
4+16=20
a^2=20
$a=\sqrt{20}$

Therefore,

$P=2(\sqrt{20}+b)$
b=5
$P=2(\sqrt{20}+5)$

Report an Error

Example Question #3 : Coordinate Geometry

New_vt_custom_xy_plane6

Identify the coordinate points for the parallelogram that is shown above.

Possible Answers:

(-2,-1), (-1,2), (3,2), (2,-1)

(-2,-2),(1,2),(3,2),(2,-1)

(-2,1), (-1,2), (-3,-2), (-2,-1)

(2,-2),(1,2),(3,2),(2,-1)

Correct answer:

(-2,-1), (-1,2), (3,2), (2,-1)

Explanation:

In order to identify the coordinate points for this parallelogram, notice that there must be two different pairs of coordinates with the same values.

Thus, the parallelogram has coordinate points: (-2,-1), (-1,2), (3,2), (2,-1)

Report an Error

Example Question #4 : Coordinate Geometry

New_vt_custom_xy_plane6

What is the area of the parallelogram shown above?

Possible Answers:

square units

Correct answer:

square units

Explanation:

To find the area of the parallelogram that is shown, apply the formula: $A=base\times height$
Since the parallelogram has a base of and a height of the solution is:
$A=4\times 3=12$

Report an Error

Example Question #5 : Geometry

New_vt_custom_xy_plane6

Given that the above parallelogram has base sides with a length of and diagonal sides with a length of $\sqrt{10}$ what is the perimeter of the parallelogram?

Possible Answers:

P=2(10+4)

$P=2(\sqrt{10}-4)$

$P=2(\sqrt{10}+4)$

$P=(\sqrt{10}+4)$

$P=2(\sqrt{10}+3)$

Correct answer:

$P=2(\sqrt{10}+4)$

Explanation:

In order to find the perimeter of the parallelogram apply the formula: P=2(a+b) , where the length of one diagonal side and the length of one base.

In this problem, $a=\sqrt{10}$ and b= 4 .
Thus, the correct answer is: $P=2(\sqrt{10}+4)$

Report an Error

Example Question #5 : Coordinate Geometry

New_vt_custom_xy_plane5

Identify the coordinate points for the parallelogram shown above.

Possible Answers:

(2,0), (4,4), (7,0), (9,4)

(-2,0), (4,4), (7,3), (9,4)

(2,5), (4,0), (7,1), (9,3)

(2,1), (4,4), (7,0), (9,-4)

Correct answer:

(2,0), (4,4), (7,0), (9,4)

Explanation:

In order to identify the coordinate points for this parallelogram, notice that there must be two different pairs of coordinates with the same values.

Thus, the correct set of coordinates is:
(2,0), (4,4), (7,0), (9,4)

Report an Error

Example Question #1 : How To Find A Rectangle On A Coordinate Plane

A shape is plotted on a coordinate axis. The endpoints are $(2,0), (9,0), (2,4), and\ (9,4)$ . What shape is it?

Possible Answers:

Triangle

Rectangle

Parallelogram

Square

Trapezoid

Correct answer:

Rectangle

Explanation:

Plot the points on a coordinate axis. Once it's graphed, you can see that there are two pairs of congruent, or equal, sides. The shape that best fits these characteristics is a rectangle.

Report an Error

Example Question #1 : How To Find A Rectangle On A Coordinate Plane

New_vt_custom_xy_plane2

Rectangle $\small ABCD$ has coordinates: $\small A(-4,-3)$ , $\small B(-4,1)$ , $\small C(3,1)$ , $\small D(3,-3)$ . Find the area of rectangle $\small ABCD$ .

Possible Answers:

$\small 28$ square units

$\small 26$ square units

$\small 11$ square units

$\small 32$ square units

Correct answer:

$\small 28$ square units

Explanation:

In order to find the area of rectangle $\small ABCD$ apply the formula: $\small A=width\times length$

Since rectangle $\small ABCD$ has a width of $\small 7$ and a length of $\small 4$ the solution is:

$\small A=7\times4=28$ square units

Report an Error

Example Question #1 : How To Find A Rectangle On A Coordinate Plane

New_vt_custom_xy_plane2

Rectangle $\small ABCD$ has coordinates: $\small A(-4,-3)$ , $\small B(-4,1)$ , $\small C(3,1)$ , $\small D(3,-3)$ . What is the perimeter?

Possible Answers:

$\small 22$

$\small 23$

$\small 11$

$\small 21$

$\small 28$

Correct answer:

$\small 22$

Explanation:

To find the perimeter of rectangle $\small ABCD$ , apply the formula: $\small p=2(width)+2(length)$

Thus, the solution is:

$\small p=2(7)+2(4)$
$\small p=14+8$
$\small p=22$

Report an Error

Example Question #1 : How To Find A Rectangle On A Coordinate Plane

Rectangle ABCD has coordinate points: A(-2,2) , B(-2,4) , C(2,4) , D(2,2) . Find the area of rectangle ABCD .

Possible Answers:

square units

Correct answer:

square units

Explanation:

The area of rectangle ABCD can be found by multiplying the width and length of the rectangle.

To find the length of the rectangle compare the x values of two of the coordinates:

Since A(-2,2), C(2,4) the length is 2-(-2)=4 .

To find the width of the rectangle we need to look at the y coordinates of two of the points.

Since A(-2,2), C(2,4) the width is 4-2=2 .

The solution is:

$A=w\times l$
$A=4\times2=8$

Report an Error

View Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

View Tutors

Jose
Certified Tutor

Old Dominion University, Current Undergrad Student, Mathematics.

View Tutors

Chase
Certified Tutor

Western Governors University, Bachelor of Science, Mathematics.

All ISEE Lower Level Quantitative Resources

20 Diagnostic Tests 114 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SSAT Tutors in Atlanta, French Tutors in Seattle, Statistics Tutors in New York City, GMAT Tutors in Los Angeles, MCAT Tutors in Miami, Physics Tutors in New York City, Math Tutors in New York City, Algebra Tutors in Dallas Fort Worth, Physics Tutors in San Francisco-Bay Area, SSAT Tutors in Los Angeles

Popular Courses & Classes

GMAT Courses & Classes in Miami, GMAT Courses & Classes in Boston, GRE Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in Phoenix, GRE Courses & Classes in Washington DC, ACT Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Washington DC, SAT Courses & Classes in Miami, SAT Courses & Classes in Denver, ISEE Courses & Classes in Phoenix

Popular Test Prep

ACT Test Prep in Los Angeles, GRE Test Prep in New York City, LSAT Test Prep in Seattle, ISEE Test Prep in Atlanta, ACT Test Prep in San Francisco-Bay Area, GRE Test Prep in Chicago, GMAT Test Prep in Dallas Fort Worth, SSAT Test Prep in Boston, GMAT Test Prep in Miami, SSAT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Lower Level Quantitative : Coordinate Geometry

Study concepts, example questions & explanations for ISEE Lower Level Quantitative

All ISEE Lower Level Quantitative Resources

Example Questions

Example Question #1 : Coordinate Geometry

Example Question #2 : Coordinate Geometry

Example Question #3 : Coordinate Geometry

Example Question #4 : Coordinate Geometry

Example Question #5 : Geometry

Example Question #5 : Coordinate Geometry

Example Question #1 : How To Find A Rectangle On A Coordinate Plane

Example Question #1 : How To Find A Rectangle On A Coordinate Plane

Example Question #1 : How To Find A Rectangle On A Coordinate Plane

Example Question #1 : How To Find A Rectangle On A Coordinate Plane

All ISEE Lower Level Quantitative Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: