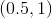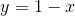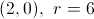All Precalculus Resources
Example Questions
Example Question #1 : Pre Calculus
Information about the Hardy Weinberg equation: http://www.nature.com/scitable/definition/hardy-weinberg-equation-299
The Hardy Weinberg equation is a very important concept in population genetics. Suppose we have two "alleles" for a specific trait (like eye color, gender, etc..) The proportion for which allele is present is given by 
Then by Hardy-Weinberg:



Which statement discribes the graph that would appropriately represents the above relation?
Curved line passing through the point
Straight line passing through the point
Parabola opening up passing through the point
Straight line passing through the point
Straight line passing through the point
The equation can be reduced by taking the square root of both sides.


As a simple test, all other values when substituted into the original equation fail. However, 

Example Question #1 : Graphing Functions
What is the center and radius of the circle indicated by the equation?
A circle is defined by an equation in the format 
The center is indicated by the point 

In the equation 


Example Question #1 : Circles
What is the equation of the circle with center at (4, -5) and a point on the circle at (4, -2)? What is the radius?
The form most often used for circles is the following general equation:

where (h, k) are the coordinates of the center and r is the radius. We are given the coordinates of the center as (4, -5), so h is 4 and k is -5.
We still need to find the radius. We can do this by plugging in the second given point, (4, -2).
Hence the formula of the circle is

and the radius is 
Example Question #3 : Conic Sections
Find the center and radius of this circle:


To solve this problem we need to get our function into the form:
where center=(h,k) and r=radius. To do this we need to complete the square with both the x an y parts of the equation
then we factor our trinomials and add our constants and we get:
so our center is 
Example Question #1 : Circles
Which function will graph a circle of radius 

The general form for the function of a circle of radius r and centered at (a,b) is:

The circle is centered at 







The final form should be:

Example Question #1 : Ellipses
Find the focal points of the conic below:
The first thing we want to do is put the conic (an ellipse because the x2 and the y2 terms have the same sign) into a better form i.e.
where (h,k) is the center of our ellipse.
We will continue by completing the square for both the x and y binomials.
First we seperate them into two trinomials:
then we pull a 27 out of the first one and a 16 out of the second
then we add the correct constant to each trinomial (being sure to add the same amount to the other side of our equation.
then we factor our trinomials and divide by 16 and 27 to get
so the center of our ellipse is (-6,3) and we calculate the distance from the focal points to the center by the equation:
and we know that our ellipse is stretched in the y direction because b>a so our focal points will be c displaced from our center.
with
our focal points are
Example Question #2 : Conic Sections
Find the center of this ellipse:
To find the center of this ellipse we need to put it into a better form. We do this by rearranging our terms and completing the square for both our y and x terms.

completing the square for both gives us this.
we could divide by 429 but we have the information we need. The center of our ellipse is
Example Question #3 : Conic Sections
What is the equation of the elipse centered at the origin and passing through the point (5, 0) with major radius 5 and minor radius 3?
The equation of an ellipse is

where a is the horizontal radius, b is the vertical radius, and (h, k) is the center of the ellipse. In this case we are told that the center is at the origin, or (0,0), so both h and k equal 0. That brings us to:
We are told about the major and minor radiuses, but the problem does not specify which one is horizontal and which one vertical. However it does tell us that the ellipse passes through the point (5, 0), which is in a horizontal line with the center, (0, 0). Therefore the horizontal radius is 5.
The vertical radius must then be 3. We can now plug these in:
Example Question #4 : Conic Sections
An ellipse is centered at (-3, 2) and passes through the points (-3, 6) and (4, 2). Determine the equation of this eclipse.
The usual form for an ellipse is

where (h, k) is the center of the ellipse, a is the horizontal radius, and b is the vertical radius.
Plug in the coordinate pair:
Now we have to find the horizontal radius and the vertical radius. Let's compare points; we are told the ellipse passes through the point (-3, 6), which is vertically aligned with the center. Therefore the vertical radius is 4.
Similarly, the ellipse passes through the point (4, 2), which is horizontally aligned with the center. This means the horizontal radius must be 7.
Substitute:
Example Question #1 : Pre Calculus
What is the shape of the graph indicated by the equation?
Hyperbola
Ellipse
Circle
Parabola
Ellipse
An ellipse has an equation that can be written in the format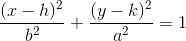
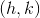

Certified Tutor
Certified Tutor
All Precalculus Resources