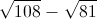\(\displaystyle \sqrt{\frac{32}{4}}\) 

There are two ways to solve this problem. First you can divide the numbers under the radical. Then simplify. 

Example 1

\(\displaystyle \sqrt{\frac{32}{4}}=\sqrt{8}=\sqrt{4}\cdot\sqrt{2}=2\sqrt{2}\)

Example 2 

Find the square root of both numerator and denominator, simplifying as much as possible then dividing out like terms. 

\(\displaystyle \sqrt{\frac{32}{4}}=\frac{\sqrt{32}}{\sqrt{4}}=\frac{\sqrt{16}\cdot \sqrt{2}}{\sqrt{4}}=\frac{4\sqrt{2}}{2}=2\sqrt{2}\)

Both methods will give you the correct answer of \(\displaystyle 2\sqrt{2}\).

√27 is the same as 3√3, while √12 is the same as 2√3.

3√3 + 2√3 = 5√3

(5√3)/(√3) = 5

To simplfy, we must first distribute the square root.

\(\displaystyle \frac{\sqrt{64}}{\sqrt{169}}\)

Next, we can simplify each of the square roots.

\(\displaystyle \frac{8}{13}\)

Find the quotient:

\(\displaystyle \frac{\sqrt{18}}{\sqrt{2}}\)

There are two ways to approach this problem.

Option 1: Combine the radicals first, the reduce

\(\displaystyle \frac{\sqrt{18}}{\sqrt{2}}=\sqrt{\frac{18}{2}}=\sqrt{9}=3\)

Option 2: Simplify the radicals first, then reduce

\(\displaystyle \frac{\sqrt{18}}{\sqrt{2}}=\frac{\sqrt{9\cdot 2}}{\sqrt{2}}=\frac{3\sqrt{2}}{\sqrt{2}}=3\)

Simplify each radical:

\(\displaystyle \frac{\sqrt{54}}{\sqrt{45}} = \frac{\sqrt{9\cdot 6}}{\sqrt{9\cdot 5}}=\frac{3\sqrt{6}}{3\sqrt{5}}=\frac{\sqrt{6}}{\sqrt{5}}\)

Rationalize the denominator:

\(\displaystyle \frac{\sqrt{6}}{\sqrt{5}} \cdot \frac{\sqrt{5}}{\sqrt{5}}= \frac{\sqrt{30}}{5}\)

Let us factor 108 and 81

\(\displaystyle 108=2\times 54= 2\times 2\times 27= 2^2\times 3\times 9= 2^2\times 3^2\times 3\)

\(\displaystyle 81=9\times 9=9^2\)

\(\displaystyle \sqrt{108}-\sqrt{81}=6\sqrt{3}-9\)

Step one: Find the greatest square factor of each radical

For \(\displaystyle 63\) this is \(\displaystyle 9\), and for \(\displaystyle 28\) it is \(\displaystyle 4\).

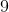
Therefore:

\(\displaystyle \sqrt{63}-\sqrt{28}=\sqrt{9*7}-\sqrt{4*7}\)

Step two: Simplify the radicals

\(\displaystyle \sqrt{9*7}-\sqrt{4*7}\)

\(\displaystyle 3\sqrt{7}-2\sqrt{7}\)

\(\displaystyle \sqrt{7}\)

\(\displaystyle \sqrt{32}+\sqrt{64}+\sqrt{8}\)

First step is to find perfect squares in all of our radicans. 

\(\displaystyle \sqrt{32}\rightarrow\sqrt{16\cdot 2}\rightarrow4\sqrt{2}\)

\(\displaystyle \sqrt{64}\rightarrow\sqrt{8\cdot 8}\rightarrow8\)

\(\displaystyle \sqrt{8}\rightarrow\sqrt{4\cdot 2}\rightarrow2\sqrt{2}\)

After doing so you are left with  \(\displaystyle 4\sqrt{2}+2\sqrt{2}+8\)

*Just like fractions you can only add together coefficents with like terms under the radical. *

\(\displaystyle 6\sqrt{2}+8\)

Square both sides:

x = (3²)² = 9² = 81

To combine radicals, they must have the same radicand. Therefore, we must find the perfect squares in each of our square roots and pull them out.

\(\displaystyle \sqrt{27}\rightarrow \sqrt{9*3}\rightarrow \sqrt{3^2*3}\rightarrow 3\sqrt{3}\)

\(\displaystyle \sqrt{48}\rightarrow \sqrt{16*3}\rightarrow \sqrt{4^2*3}\rightarrow 4\sqrt{3}\)

\(\displaystyle \sqrt{81}\rightarrow\sqrt{9*9}\rightarrow\sqrt{9^2}\rightarrow9\)

Now, we plug these equivalent expressions back into our equation and simplify:

\(\displaystyle \sqrt{27}-\sqrt{48}+\sqrt{81}\)

\(\displaystyle 3\sqrt3-4\sqrt3+9\)

\(\displaystyle -\sqrt3+9\)