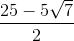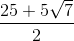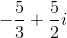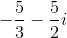We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math I : SAT Subject Test in Math I

Study concepts, example questions & explanations for SAT II Math I

Create An Account

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Types Of Numbers

Express 374 in base six.

Possible Answers:

$1402_{\textrm{six}}$

$1422_{\textrm{six}}$

$1502_{\textrm{six}}$

$1522_{\textrm{six}}$

Correct answer:

$1422_{\textrm{six}}$

Explanation:

To convert a base ten number to base six, divide the number by six, with the remainder being the digit in the units place; continue, dividing each successive quotient by 6 and putting the remainder in the next position to the left until the final quotient is less than 6.

$374 \div 6 = 62\textrm{ R }\underline{2}$ - the rightmost digit is 2

$62 \div 6 = 10 \textrm{ R }\underline{2}$ - the next digit to the left is 2

$10 \div 6 = \underline{1} \textrm{ R }\underline{4}$ - the next digit to the left is 4, and the digit to the left of that is 1.

$374 = 1422_{\textrm{six}}$

Report an Error

Example Question #2 : Types Of Numbers

Express $13241 _{\textrm{five}}$ in base ten.

Possible Answers:

1,071

921

1,021

1,121

971

Correct answer:

1,071

Explanation:

Place values in the base five system are powers of five rather than powers of ten. $13241 _{\textrm{five}}$ is equal to

$1 \times 5^{4} + 3 \times 5 ^{3} + 2 \times 5^{2} + 4 \times 5 + 1$

$= 1 \times 625 + 3 \times 125 + 2 \times 25 + 4 \times 5 + 1$

= 625 +375 + 50 + 20 + 1 = 1,071

Report an Error

Example Question #3 : Types Of Numbers

Which of the following is the smallest prime number: 8,9,11,13,17 ?

Possible Answers:

Correct answer:

Explanation:

A prime number has only two factor, and itself.

This is not true for 8 (2*4=8) or 9 (3*3*=9) so they are not the answer.

11, 13, 17 are all prime numbers and is the smallest so it is your answer.

Report an Error

Example Question #1 : Sat Subject Test In Math I

Which of the following is a rational number?

$\frac{1}{2},\sqrt{5},2i,3.658$

Possible Answers:

3.658

$\sqrt{5}$

None

$\frac{1}{2}$

Correct answer:

$\frac{1}{2}$

Explanation:

A rational number is any number that can be expressed as an integer p or a fraction p/q. In the set of number given only $\tiny \frac{1}{2}$ fits into that category.

Report an Error

Example Question #1 : Irrational Numbers

Which of the following is not an irrational number?

Possible Answers:

$\sqrt[5]{125}$

$\sqrt[3]{125}$

$\sqrt[4]{125}$

$\sqrt[6]{125}$

$\sqrt[2]{125}$

Correct answer:

$\sqrt[3]{125}$

Explanation:

A root of an integer is one of two things, an integer or an irrational number. By testing all five on a calculator, only $\sqrt[3]{125}$ comes up an exact integer - 5. This is the correct choice.

Report an Error

Example Question #2 : Irrational Numbers

Simplify by rationalizing the denominator:

$\frac{45}{5 + \sqrt{7}}$

Possible Answers:

$\frac{ 25 + 5 \sqrt{7} }{ 2}$

$\frac{ 25 - \sqrt{7} }{ 2}$

$\frac{ 25 - 5 \sqrt{7} }{ 2}$

$\frac{15 \sqrt{7}}{4}$

$\frac{ 25 + \sqrt{7} }{ 2}$

Correct answer:

$\frac{ 25 - 5 \sqrt{7} }{ 2}$

Explanation:

Multiply the numerator and the denominator by the conjugate of the denominator, which is $5 - \sqrt{7}$ . Then take advantage of the distributive properties and the difference of squares pattern:

$\frac{45}{5 + \sqrt{7}}$

$= \frac{45\left (5 - \sqrt{7} \right )}{\left (5 + \sqrt{7} \right )\left (5 - \sqrt{7} \right )}$

$= \frac{45\left (5 - \sqrt{7} \right )}{ 5 ^{2}- \left ( \sqrt{7} \right ) ^{2} }$

$= \frac{45\left (5 - \sqrt{7} \right )}{ 25 -7}$

$= \frac{45\left (5 - \sqrt{7} \right )}{ 18}$

$= \frac{5\left (5 - \sqrt{7} \right )}{ 2}$

$= \frac{ 25 - 5 \sqrt{7} }{ 2}$

Report an Error

Example Question #1 : Irrational Numbers

$\frac{-5+10i}{3+4i}=?$

Possible Answers:

1+2i

-1+2i

$-\frac{5}{3}+\frac{5}{2}i$

1-2i

$-\frac{5}{3}-\frac{5}{2}i$

Correct answer:

1+2i

Explanation:

$\frac{-5+10i}{3+4i}$

$=\frac{(-5+10i)(3-4i)}{(3+4i)(3-4i)}$

$=\frac{-15+20i+30i-40i^{2}}{9-16i^{2}}$

$=\frac{-15+50i+40}{9+16}$

$=\frac{25+50i}{25}$

=1+2i

Report an Error

Example Question #1 : Imaginary Numbers

Multiply:

(7 + 3i) (1 - 2i)

Possible Answers:

13 - 11i

7 - 5i

1 - 11i

13 - 17i

7 - 17i

Correct answer:

13 - 11i

Explanation:

Use the FOIL technique:

(7 + 3i) (1 - 2i)

$= 7 \cdot 1 - 7 \cdot 2i + 3i \cdot 1 - 3i \cdot 2i$

$= 7 - 14i + 3i - 6i ^{2}$

= 7 - 14i + 3i - 6(-1)

= 7 - 14i + 3i +6

= 13 - 11i

Report an Error

Example Question #61 : Complex Imaginary Numbers

Evaluate:

$\left (2 + 3i \right )^{3}$

Possible Answers:

-46 + 63 i

-62 + 63 i

-4 6+ 9i

8 + 9i

8 - 27i

Correct answer:

-4 6+ 9i

Explanation:

We can set A = 2, B = 3i in the cube of a binomial pattern:

$\left ( A + B\right ) ^{3} = A ^{3} + 3 A^{2 }B + 3AB^{2} + B^{3}$

$= 2 ^{3} + 3 \cdot 2 ^{2 } \cdot 3i + 3 \cdot 2 \cdot (3i)^{2} + (3i)^{3}$

$= 2^{3} + 3 \cdot 2^{2} \cdot 3i + 3 \cdot 2 \cdot 3 ^{2}\cdot i^{2} + 3^{3} \cdot i^{3}$

$= 8 + 36i + 54 i^{2} + 27 i^{3}$

= 8 + 36i + 54 (-1) + 27 (-i)

= 8 + 36i - 54 - 27 i

= -46 + 9i

Report an Error

Example Question #1 : Imaginary Numbers

Evaluate $\small \frac{-6+2i}{10-3i}$

Possible Answers:

You cannot divide by complex numbers

$\small \small \frac{-66+2i}{91-60i}$

$\small \frac{-54+38i}{109}$

$\small \small \frac{-54+38i}{91-60i}$

$\small \frac{-66+2i}{109}$

Correct answer:

$\small \frac{-66+2i}{109}$

Explanation:

To divide by a complex number, we must transform the expression by multiplying it by the complex conjugate of the denominator over itself. In the problem, $\small 10-3i$ is our denominator, so we will multiply the expression by $\small \frac{10+3i}{10+3i}$ to obtain:

$\small \frac{-6+2i}{10-3i}\frac{10+3i}{10+3i}=\frac{-60+20i-18i+6i^2}{100-30i+30i-9i^2}$ .

We can then combine like terms and rewrite all $\small i^2$ terms as $\small -1$ . Therefore, the expression becomes:

$\small \frac{-60+2i+6i^2}{100-9i^2}=\frac{-66+2i}{109}$

Our final answer is therefore $\small \frac{-66+2i}{109}$

Report an Error

View SAT Subject Test in Mathematics Level 1 Tutors

James
Certified Tutor

University of Georgia, Bachelor in Arts, Political Science and Government.

View SAT Subject Test in Mathematics Level 1 Tutors

Benjamin
Certified Tutor

Portland State University, Bachelor of Science, Computer Science.

View SAT Subject Test in Mathematics Level 1 Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Calculus Tutors in Los Angeles, Chemistry Tutors in Denver, French Tutors in Miami, Statistics Tutors in Los Angeles, Math Tutors in San Diego, LSAT Tutors in Washington DC, English Tutors in Chicago, Math Tutors in Dallas Fort Worth, Reading Tutors in Houston, Biology Tutors in Denver

Popular Courses & Classes

GRE Courses & Classes in Phoenix, ISEE Courses & Classes in Phoenix, ACT Courses & Classes in Washington DC, SSAT Courses & Classes in Los Angeles, LSAT Courses & Classes in Denver, MCAT Courses & Classes in Los Angeles, ACT Courses & Classes in Seattle, GRE Courses & Classes in Houston, MCAT Courses & Classes in Chicago, ISEE Courses & Classes in San Francisco-Bay Area

Popular Test Prep

LSAT Test Prep in Chicago, SAT Test Prep in Los Angeles, ISEE Test Prep in New York City, SSAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Houston, LSAT Test Prep in San Diego, ACT Test Prep in San Diego, GRE Test Prep in Phoenix, SSAT Test Prep in Philadelphia, ISEE Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math I : SAT Subject Test in Math I

Study concepts, example questions & explanations for SAT II Math I

All SAT II Math I Resources

Example Questions

Example Question #1 : Types Of Numbers

Example Question #2 : Types Of Numbers

Example Question #3 : Types Of Numbers

Example Question #1 : Sat Subject Test In Math I

Example Question #1 : Irrational Numbers

Example Question #2 : Irrational Numbers

Example Question #1 : Irrational Numbers

Example Question #1 : Imaginary Numbers

Example Question #61 : Complex Imaginary Numbers

Example Question #1 : Imaginary Numbers

All SAT II Math I Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: