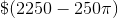We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : How to find the area of a sector

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Area Of A Sector

A circular, 8-slice pizza is placed in a square box that has dimensions four inches larger than the diameter of the pizza. If the box covers a surface area of 256 in², what is the surface area of one piece of pizza?

Possible Answers:

36π in²

18π in²

4.5π in²

144π in²

9π in²

Correct answer:

4.5π in²

Explanation:

The first thing to do is calculate the dimensions of the pizza box. Based on our data, we know 256 = s². Solving for s (by taking the square root of both sides), we get 16 = s (or s = 16).

Now, we know that the diameter of the pizza is four inches less than 16 inches. That is, it is 12 inches. Be careful! The area of the circle is given in terms of radius, which is half the diameter, or 6 inches. Therefore, the area of the pizza is π * 6² = 36π in². If the pizza is 8-slices, one slice is equal to 1/8 of the total pizza or (36π)/8 = 4.5π in².

Report an Error

Example Question #1 : Circles

If B is a circle with line AC = 12 and line BC = 16, then what is the area formed by DBE?

Possible Answers:

$200$

$144$

$100\pi$

$256\pi$

$5\pi$

Correct answer:

$100\pi$

Explanation:

Line AB is a radius of Circle B, which can be found using the Pythagorean Theorem:

$AB^2=AC^2+BC^2\rightarrow AB=\sqrt{AC^2+BC^2}=\sqrt{16^2+12^2}=\sqrt{400}=20$

Since AB is a radius of B, we can find the area of circle B via:

$Area=\pi R^2=\pi(20^2)=400\pi$

Angle DBE is a right angle, and therefore $\frac{1}{4}$ of the circle so it follows:

$Area(DBE)=\frac{400}{4}\pi=100\pi$

Report an Error

Example Question #2 : How To Find The Area Of A Sector

Circle

The radius of the circle above is and $\angle A=45^{\circ}$ . What is the area of the shaded section of the circle?

Possible Answers:

$16\pi$

$2\pi$

$4\pi$

$\pi$

$8\pi$

Correct answer:

$2\pi$

Explanation:

Area of Circle = πr² = π4²= 16π

Total degrees in a circle = 360

Therefore 45 degree slice = 45/360 fraction of circle = 1/8

Shaded Area = 1/8 * Total Area = 1/8 * 16π = 2π

Report an Error

Example Question #261 : Geometry

Square-missing

SRAD is a square.

$\overline{AB}=\overline{BC}=\overline{CD}$

The arc from to is a semicircle with a center at the midpoint of $\overline{BC}$ .

All units are in feet.

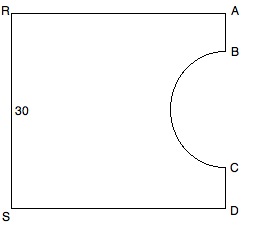
The diagram shows a plot of land.

The cost of summer upkeep is $2.50 per square foot.

In dollars, what is the total upkeep cost for the summer?

Possible Answers:

$\$(2250-250\pi )$

$\$(2250-31.25\pi )$

$\$(900-12.5\pi )$

$\$(900-25\pi )$

$\$900$

Correct answer:

$\$(2250-31.25\pi )$

Explanation:

To solve this, we must begin by finding the area of the diagram, which is the area of the square less the area of the semicircle.

The area of the square is straightforward:

30 * 30 = 900 square feet

Because each side is 30 feet long, AB + BC + CD = 30.

We can substitute BC for AB and CD since all three lengths are the same:

BC + BC + BC = 30

3BC = 30

BC = 10

Therefore the diameter of the semicircle is 10 feet, so the radius is 5 feet.

The area of the semi-circle is half the area of a circle with radius 5. The area of the full circle is 5²π = 25π, so the area of the semi-circle is half of that, or 12.5π.

The total area of the plot is the square less the semicircle: 900 - 12.5π square feet

The cost of upkeep is therefore 2.5 * (900 – 12.5π) = $(2250 – 31.25π).

Report an Error

Example Question #11 : Circles

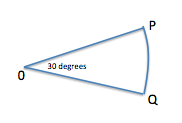
In the figure, PQ is the arc of a circle with center O. If the area of the sector is $3\pi$ what is the perimeter of sector?

Possible Answers:

$12 + \pi$

$12 + 2\pi$

$3 + 2\pi$

$6 + \pi$

$1 + \pi$

Correct answer:

$12 + \pi$

Explanation:

First, we figure out what fraction of the circle is contained in sector OPQ: $\frac{30^{\circ}}{360^{\circ}}= \frac{1}{12}$ , so the total area of the circle is $\dpi{100} \small 12\times 3\pi=36$ .

Using the formula for the area of a circle, ${\pi}r^{2}$ , we can see that $\dpi{100} \small r=6$ .

We can use this to solve for the circumference of the circle, $2{\pi}r$ , or $12{\pi}$ .

Now, OP and OQ are both equal to r, and PQ is equal to $\dpi{100} \small \frac{1}{12}$ of the circumference of the circle, or ${\pi}$ .

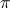
To get the perimeter, we add OP + OQ + PQ, which give us $12+{\pi}$ .

Report an Error

Example Question #261 : Plane Geometry

A central angle of a circle measures 60 degrees. If its corresponding arc measures 3 units, what is the area of the circle?

Possible Answers:

$18\pi$

$\frac{81}{\pi }$

$9\pi$

$\frac{9}{\pi}$

Correct answer:

$\frac{81}{\pi }$

Explanation:

If the central angle measures 60 degrees, divide the 360 total degrees in the circle by 60.

$\frac{360}{60}=6$

Multiply this by the measure of the corresponding arc to find the total circumference of the circle.

$3\times 6 =18$

Use the circumference to find the radius, then use the radius to find the area.

$C=2\pi r$

$18=2\pi r$

$\frac{18}{2\pi}=r$

$\frac{9}{\pi}=r$

$A=\pi r^2$

$A=\pi\times (\frac{9}{\pi})^2$

$A= \pi \times \frac{81}{\pi^2}$

$A = \frac{81\pi}{\pi^2}$

$A=\frac{81}{\pi}$

Report an Error

View SAT Mathematics Tutors

Noah
Certified Tutor

Bard College, Bachelors, Philosophy and Creative Writing (Dual Major). Sarah Lawrence College, Master of Fine Arts, Creative ...

View SAT Mathematics Tutors

Priyanka
Certified Tutor

CUNY Hunter College, Bachelor in Arts, Economics.

View SAT Mathematics Tutors

Joy
Certified Tutor

Boston University, Bachelor in Arts, Conservation Biology.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

SSAT Courses & Classes in Phoenix, GRE Courses & Classes in Phoenix, MCAT Courses & Classes in Washington DC, SAT Courses & Classes in Houston, LSAT Courses & Classes in San Diego, SAT Courses & Classes in Denver, ISEE Courses & Classes in Atlanta, ISEE Courses & Classes in Phoenix, GMAT Courses & Classes in Miami, ACT Courses & Classes in Philadelphia

Popular Test Prep

SSAT Test Prep in Houston, SAT Test Prep in San Diego, ACT Test Prep in Chicago, ACT Test Prep in Los Angeles, GRE Test Prep in Phoenix, ISEE Test Prep in Denver, ACT Test Prep in Miami, LSAT Test Prep in San Diego, GRE Test Prep in Seattle, MCAT Test Prep in Los Angeles

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : How to find the area of a sector

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #1 : How To Find The Area Of A Sector

Example Question #1 : Circles

Example Question #2 : How To Find The Area Of A Sector

Example Question #261 : Geometry

Example Question #11 : Circles

Example Question #261 : Plane Geometry

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: