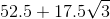We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : How to find the perimeter of a right triangle

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Perimeter Of A Right Triangle

Three points in the xy-coordinate system form a triangle.

The points are (-1,5) (-1,1) (4,5) .

What is the perimeter of the triangle?

Possible Answers:

$9 + \sqrt{26}$

$9 + \sqrt{41}$

$9 + \sqrt{71}$

Correct answer:

$9 + \sqrt{41}$

Explanation:

Drawing points gives sides of a right triangle of 4, 5, and an unknown hypotenuse.

Using the pythagorean theorem we find that the hypotenuse is $\sqrt{41}$ .

Report an Error

Example Question #11 : Triangles

Triangle

Based on the information given above, what is the perimeter of triangle ABC?

Possible Answers:

$35+17.5\sqrt{2}$

$17.5+17.5\sqrt{3}$

$52.5\sqrt{3}$

$306.25\sqrt{3}$

$52.5+17.5\sqrt{3}$

Correct answer:

$52.5+17.5\sqrt{3}$

Explanation:

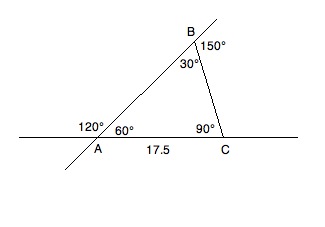
Triangle-solution

Consult the diagram above while reading the solution. Because of what we know about supplementary angles, we can fill in the inner values of the triangle. Angles A and B can be found by the following reductions:

A + 120 = 180; A = 60

B + 150 = 180; B = 30

Since we know A + B + C = 180 and have the values of A and B, we know:

60 + 30 + C = 180; C = 90

This gives us a 30:60:90 triangle. Now, since 17.5 is across from the 30° angle, we know that the other two sides will have to be √3 and 2 times 17.5; therefore, our perimeter will be as follows:

$17.5+2(17.5)+17.5\sqrt{3}=52.2+17.5\sqrt{3}$

Report an Error

Example Question #43 : Geometry

Right triangle 7

Give the perimeter of the provided triangle.

Possible Answers:

$24+ 12 \sqrt{3}$

$24+ 12 \sqrt{5}$

$24+ 12\sqrt{2}$

Correct answer:

$24+ 12\sqrt{2}$

Explanation:

The figure shows a right triangle. The acute angles of a right triangle have measures whose sum is $90^{\circ }$ , so

$m \angle A+ m \angle C = 90^{\circ }$

Substituting $45^{\circ }$ for $m \angle C$ :

$m \angle A+ 45^{\circ } = 90^{\circ }$

$m \angle A= 45^{\circ }$

This makes $\bigtriangleup ABC$ a 45-45-90 triangle.

By the 45-45-90 Triangle Theorem, legs $\overline{AB}$ and $\overline{BC}$ are of the same length, so

BC = AB = 12 .

Also by the 45-45-90 Triangle Theorem, the length of hypotenuse $\overline{AC}$ is equal to that of leg $\overline{BC}$ multiplied by $\sqrt{2}$ . Therefore,

$AC = AB \cdot \sqrt{2} = 12 \sqrt{2}$ .

The perimeter of the triangle is

$P = AB + B C + AC = 12+ 12+ 12 \sqrt{2} = 24 + 12 \sqrt{2}$

Report an Error

Example Question #44 : Geometry

Right triangle 7

What is the perimeter of the triangle above?

Possible Answers:

$12+12 \sqrt{2}$

$12+ 12\sqrt{3}$

$12+ 8\sqrt{3}$

Correct answer:

$12+12 \sqrt{2}$

Explanation:

The figure shows a right triangle. The acute angles of a right triangle have measures whose sum is $90^{\circ }$ , so

$m \angle A+ m \angle C = 90^{\circ }$

Substituting $45^{\circ }$ for $m \angle C$ :

$m \angle A+ 45^{\circ } = 90^{\circ }$

$m \angle A= 45^{\circ }$

This makes $\bigtriangleup ABC$ a 45-45-90 triangle. By the 45-45-90 Triangle Theorem, the length of leg $\overline{BC}$ is equal to that of hypotenuse $\overline{AC}$ , the length of which is 12, divided by $\sqrt{2}$ . Therefore,

$BC = \frac{AC}{\sqrt{2}} = \frac{12}{\sqrt{2}}$

Rationalize the denominator by multiplying both halves of the fraction by $\sqrt{2}$ :

$BC = \frac{12 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{12 \sqrt{2}}{2} = 6 \sqrt{2}$

By the same reasoning, $AB= 6 \sqrt{2}$ .

The perimeter of the triangle is

P = AB + B C + AC

$P= 6 \sqrt{2} + 6 \sqrt{2} + 12 = 12+ 12 \sqrt{2}$

Report an Error

View SAT Mathematics Tutors

Nicholas
Certified Tutor

Fordham University, Bachelors, Business Administration and Management. Boston University, Masters, Media Ventures.

View SAT Mathematics Tutors

Scott
Certified Tutor

Rutgers College, Bachelors, Political Science and Government. Florida Coastal School of Law, PHD, Law.

View SAT Mathematics Tutors

Noah
Certified Tutor

Bard College, Bachelors, Philosophy and Creative Writing (Dual Major). Sarah Lawrence College, Master of Fine Arts, Creative ...

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

GMAT Courses & Classes in Denver, SSAT Courses & Classes in San Diego, GMAT Courses & Classes in Houston, LSAT Courses & Classes in Denver, ACT Courses & Classes in Seattle, ISEE Courses & Classes in Denver, GMAT Courses & Classes in Washington DC, LSAT Courses & Classes in San Diego, GRE Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Phoenix

Popular Test Prep

ISEE Test Prep in Philadelphia, SAT Test Prep in Boston, GMAT Test Prep in Denver, GRE Test Prep in Phoenix, LSAT Test Prep in San Diego, ISEE Test Prep in Seattle, GMAT Test Prep in Houston, GMAT Test Prep in Dallas Fort Worth, ISEE Test Prep in Boston, ISEE Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : How to find the perimeter of a right triangle

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #1 : How To Find The Perimeter Of A Right Triangle

Example Question #11 : Triangles

Example Question #43 : Geometry

Example Question #44 : Geometry

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: