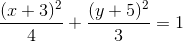All SSAT Upper Level Math Resources
Example Questions
Example Question #1 : How To Find The Equation Of A Curve
If the 


Write the slope-intercept form.
The point given the x-intercept of 6 is 
Substitute the point and the slope into the equation and solve for the y-intercept.
Substitute the y-intercept back to the slope-intercept form to get your equation.
Example Question #502 : Ssat Upper Level Quantitative (Math)
A vertical parabola on the coordinate plane has vertex 


Give its equation.
Insufficient information is given to determine the equation.
The equation of a vertical parabola, in vertex form, is

where 

To find 


The equation, in vertex form, is 
Example Question #1 : How To Find The Equation Of A Curve
A vertical parabola on the coordinate plane has vertex 


Give its equation.
Insufficient information is given to determine the equation.
The equation of a vertical parabola, in vertex form, is

where 

To find 


The equation, in vertex form, is 
Example Question #231 : Coordinate Geometry
A vertical parabola on the coordinate plane has 



Give its equation.
Insufficient information is given to determine the equation.
If a vertical parabola has only one 

The equation of a vertical parabola, in vertex form, is

where 

To find 


The equation, in vertex form, is 
Example Question #2 : How To Find The Equation Of A Curve
A vertical parabola on the coordinate plane has 



Give its equation.
Insufficient information is given to determine the equation.
Insufficient information is given to determine the equation.
The equation of a vertical parabola, in standard form, is
for some real 




Set 
However, no other information is given, so the values of 

Example Question #511 : Ssat Upper Level Quantitative (Math)

Give the equation of the above ellipse.
The equation of the ellipse with center 


The ellipse has center 



The equation of the ellipse is
Example Question #512 : Ssat Upper Level Quantitative (Math)

Give the equation of the above ellipse.
The equation of the ellipse with center 


The ellipse has center 



The equation of the ellipse is
Example Question #231 : Coordinate Geometry

Give the equation of the above ellipse.
The equation of the ellipse with center 


The ellipse has center 



The equation of the ellipse is
Example Question #232 : Coordinate Geometry
The 




Insufficient information is given to determine the equation.
To find the 




The 

The 
The 

The parabola has these intercepts as well. Also, since the vertical parabola has only one 
The equation of a vertical parabola, in vertex form, is

where 

for some real 

The parabola has equation 
Example Question #233 : Coordinate Geometry
An ellipse on the coordinate plane has as its center the point 


Insufficient information is given to determine the equation.
The equation of the ellipse with center 


The center is 


To find 











The equation is
or

Certified Tutor
All SSAT Upper Level Math Resources














![y = a[x-(-4)]^{2}+10](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/349648/gif.latex)














![y = a[x-(-3)]^{2}+ (-6)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/349578/gif.latex)