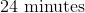All Algebra II Resources
Example Questions
Example Question #1 : Simplifying Equations
Simplify.
a. Begin by using the FOIL method to square (2x-2).
The resulting equation should be:
b. Distribute -5 to the expression inside the parentheses to get
c. Finish simplifying by combining like terms:
Example Question #462 : Basic Single Variable Algebra
Betty is working on increasing the number of minutes that she can run consecutively. Each time she goes for a jog she runs 



If Betty increases her time by 2 minutes 3 times a week, then she increases her time by a total of 6 minutes per week. We also know that she starts out running for 20 minutes. We can use this information to set up the equation in 
Here x is the number of weeks, and y is the number of minutes she can run at the end of each week. The question is asking for how many minutes she can run at the end of 2 weeks, so we plug in 2 for x:
Example Question #463 : Basic Single Variable Algebra
Brian places an order for 





We can set up a system of equations to solve this problem. If we call the price of a single pair of socks "s" and a single belt "b" then we can set up the following equations:
The easiest way to solve this system would be to combine them in such a way that eliminates one of the variables. We can do this by multiplying the bottom equation by -2, then adding it to the top equation.
This simplifies to:
Now when we add it to the first equation, the s variables will cancel out:
_____________________
We can now solve for b, then plug that value into either one of the original equations.
Thus, we get that the cost of a belt, b, is 10 dollars and the cost of a pair of socks, s, is 5 dollars.
Example Question #464 : Basic Single Variable Algebra
They say it takes 







Anna; Anna will take 

Anna; Anna will take 

Maggie; Maggie will take 

Maggie; Maggie will take 

Anna; Anna will take 

Anna; Anna will take 

The number of hours that Anna practices per week can be found by:
If Anna practices for 4.5 hours per week, then the number of weeks it will take for her to reach 10,000 hours can by found by:
We can use the same process to find the number of hours that Maggie practices per week, and from there the number of weeks it will take her to reach 10,000 hours:
Example Question #2 : Simplifying Equations
Dave starts biking at 


Mike will never catch up to Dave.
The equation for Dave's distance after t hours can be written as:
Since Mike is biking for half an hour less than Dave, we can write his distance as:
We want to know how many hours it takes for Mike to catch up to Dave. In other words, we are looking for the time when they have traveled the same distance. So, we can set the equations for distance traveled equal to each other:
"t" is how long Dave bikes for until Mike catches up. "t-.5" is the amount of time that Mike bikes for, and that is what we are trying to find.
So, Mike bikes for 5/6 hours until he catches up with Dave.
Example Question #3 : Simplifying Equations
Simplify
Rearrange the terms by grouping like terms together:


Finally, move the numerical terms to the other side of the equation so that all of the like terms are together:


Example Question #1 : Simplifying Equations
Simplify and solve:
Add 
Subtract four from both sides.
Divide by twelve on both sides.
Reduce.
Example Question #111 : Equations
Simplify the equation and solve:
Use order of operations to expand the terms of the parenthesis first.
Rewrite the equation.
Simplify the left side of the equation.
Add ten on both sides of the equation.
Simplify.
The answer is:
Example Question #3 : Simplifying Equations
Solve for 


In order to isolate the 

Distribute 
Subtract five on both sides.
Add 

Take out a common factor of 
Divide by 
The answer is:
Example Question #4 : Simplifying Equations
Simplify:
To simplify:
1. Factor out 

2. Reduce the equation and the final solution is:
Certified Tutor
Certified Tutor
All Algebra II Resources