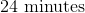a. Begin by using the FOIL method to square (2x-2).

The resulting equation should be: \(\displaystyle -5(4x^2-8x+4)+12x-6\)

b. Distribute -5 to the expression inside the parentheses to get \(\displaystyle (-20x^2+40x-20)+12x-6\)

c. Finish simplifying by combining like terms:

\(\displaystyle -20x^2+(40x+12x)+(-20-6)=-20x^2+52x-26\)

If Betty increases her time by 2 minutes 3 times a week, then she increases her time by a total of 6 minutes per week. We also know that she starts out running for 20 minutes. We can use this information to set up the equation in \(\displaystyle y=mx+b\) form as:

\(\displaystyle y=6x+20\)

Here x is the number of weeks, and y is the number of minutes she can run at the end of each week. The question is asking for how many minutes she can run at the end of 2 weeks, so we plug in 2 for x:

\(\displaystyle y=6(2)+20\)

\(\displaystyle y=12+20\)

\(\displaystyle y=32\)

We can set up a system of equations to solve this problem. If we call the price of a single pair of socks "s" and a single belt "b" then we can set up the following equations:

\(\displaystyle 8s+3b=70\)

\(\displaystyle 4s+7b=90\)

The easiest way to solve this system would be to combine them in such a way that eliminates one of the variables. We can do this by multiplying the bottom equation by -2, then adding it to the top equation.

\(\displaystyle -2(4s+7b=90)\)

This simplifies to:

\(\displaystyle -8s-14b=-180\)

Now when we add it to the first equation, the s variables will cancel out:

\(\displaystyle 8s+3b=70\)

\(\displaystyle -8s-14b=-180\)

_____________________

\(\displaystyle -11b=-110\)

We can now solve for b, then plug that value into either one of the original equations.

\(\displaystyle b=10\)

\(\displaystyle 4s+7(10)=90\)

\(\displaystyle 4s=20\)

\(\displaystyle s=5\)

Thus, we get that the cost of a belt, b, is 10 dollars and the cost of a pair of socks, s, is 5 dollars.

The number of hours that Anna practices per week can be found by:

\(\displaystyle 45 \times 6=270 \text{ min}\)

\(\displaystyle \frac{270 \text{ min}}{60}=4.5 \text{ hours}\)

If Anna practices for 4.5 hours per week, then the number of weeks it will take for her to reach 10,000 hours can by found by:

\(\displaystyle \frac{10,000}{4.5}\approx 2,222\)

We can use the same process to find the number of hours that Maggie practices per week, and from there the number of weeks it will take her to reach 10,000 hours:

\(\displaystyle 30\times 7=210 \text{ min}\)

\(\displaystyle \frac{210 \text{ min}}{60}=3.5 \text{ hours}\)

\(\displaystyle \frac{10,000}{3.5}\approx 2,857\)

The equation for Dave's distance after t hours can be written as:

\(\displaystyle d=5t\)

Since Mike is biking for half an hour less than Dave, we can write his distance as:

\(\displaystyle d=8(t-.5)\)

We want to know how many hours it takes for Mike to catch up to Dave. In other words, we are looking for the time when they have traveled the same distance. So, we can set the equations for distance traveled equal to each other:

\(\displaystyle 5t=8(t-.5)\)

\(\displaystyle 5t=8t-4\)

\(\displaystyle 4=3t\)

\(\displaystyle t=\frac{4}{3}\text{ hours}\)

"t" is how long Dave bikes for until Mike catches up. "t-.5" is the amount of time that Mike bikes for, and that is what we are trying to find.

\(\displaystyle \frac{4}{3}-\frac{1}{2}=\frac{8}{6}-\frac{3}{6}=\frac{5}{6}\)

So, Mike bikes for 5/6 hours until he catches up with Dave.

Rearrange the terms by grouping like terms together: 

\(\displaystyle x^2+3x^2+x+y-4y-13+2=14,\) then simplify: 

\(\displaystyle 4x^2+x-3y-11=14\).

Finally, move the numerical terms to the other side of the equation so that all of the like terms are together: 

\(\displaystyle 4x^2+x-3y-11+11=14+11\), then simplify: \(\displaystyle 4x^2+x-3y=25\).

Add \(\displaystyle 3x\) on both sides of the equation.

\(\displaystyle 6-3x +(3x) = 9x+4+(3x)\)

\(\displaystyle 6= 12x+4\)

Subtract four from both sides.

\(\displaystyle 6-(4)= 12x+4-(4)\)

\(\displaystyle 2=12x\)

Divide by twelve on both sides.

\(\displaystyle \frac{2}{12}=\frac{12x}{12}\)

Reduce.

\(\displaystyle x=\frac{1}{6}\)

Use order of operations to expand the terms of the parenthesis first.

\(\displaystyle 3(x-2)=3x-6\)

Rewrite the equation.

\(\displaystyle 3x-6-4=6\)

Simplify the left side of the equation.

\(\displaystyle 3x-10=6\)

Add ten on both sides of the equation.

\(\displaystyle 3x-10+10=6+10\)

Simplify.

\(\displaystyle 3x=16\)

The answer is:  \(\displaystyle x=\frac{16}{3}\)

In order to isolate the \(\displaystyle x\) variable, we will need to use order of operations to eliminate the parentheses and group the terms with an \(\displaystyle x\) variable to one side of the equation.

Distribute \(\displaystyle 2x\) inside the parentheses.

\(\displaystyle 2xy+2xz+5 = 7-x\)

Subtract five on both sides.

\(\displaystyle 2xy+2xz= 2-x\)

Add \(\displaystyle x\) on both sides to move the negative \(\displaystyle x\) to the left side.

\(\displaystyle 2xy+2xz+x= 2\)

Take out a common factor of \(\displaystyle x\) on the left side.

\(\displaystyle x(2y+2z+1)= 2\)

Divide by \(\displaystyle 2y+2z+1\) on both sides of the equation.

The answer is:  \(\displaystyle x= \frac{2}{2y+2z+1}\)

To simplify:

\(\displaystyle \frac{2x^{2}+24x}{2x}\)

1. Factor out \(\displaystyle 2x\) from \(\displaystyle 2x^{2}+24x\) and we will get:

\(\displaystyle \frac{2x(x+12)}{2x}\)

2. Reduce the equation and the final solution is:

\(\displaystyle x+12\)