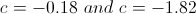Call Now to Set Up Tutoring:

(888) 888-0446

Calculus 1 : How to graph functions of points

Study concepts, example questions & explanations for Calculus 1

Create An Account

All Calculus 1 Resources

10 Diagnostic Tests 438 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Graph Functions Of Points

Find the critical points (rounded to two decimal places):

f(x)= x^3+3x^2+x

Possible Answers:

$c=-0.25\ and\ c=-2.41$

$c=0.18\ and\ c=1.82$

$c=0.25\ and\ c=2.41$

$c=-0.18\ and\ c=-1.82$

Correct answer:

$c=-0.18\ and\ c=-1.82$

Explanation:

To find the critical points, set f{}'(x)=0 and solve for .

f(x)= x^3+3x^2+x

Differentiate:

$f{}'(x)= 3x^2+6x+1$

Set equal to zero:

3x^2+6x+1=0

Solve for using the quadratic formula: $x= \frac{-b\pm \sqrt{b^2-4ac}}{2a}$

$a=3,\ b=6,\ c=1$

$x= \frac{-6\pm \sqrt{(6)^2-4(3)(1)}}{2(3)}$

$x= \frac{-6\pm \sqrt{36-12}}{6}}$

$x= \frac{-6+\sqrt{24}}{6}}\ and\ x= \frac{-6-\sqrt{24}}{6}}$

$c=-0.18\ and\ c=-1.82$

Report an Error

Example Question #2 : How To Graph Functions Of Points

Find the value(s) of the critical point(s) of

f(x)=x^3+2x^2+x+4 .

Possible Answers:

$\\ c_1=3 \\ \\ c_2=-1$

There are no real answers.

$\\ c_1=\frac{1}{3} \\ \\ c_2=1$

$\\ c_1=-3 \\ \\ c_2=1$

$\\ c_1=-\frac{1}{3} \\ \\ c_2=-1$

Correct answer:

$\\ c_1=-\frac{1}{3} \\ \\ c_2=-1$

Explanation:

In order to find the critical points, we must find $\ f'(x)$ and solve for $\ x$

f(x)=x^3+2x^2+x+4

$\\ \\ f'(x)=3x^2+4x+1$

Set f'(x)=0

$\\ \\ 3x^2+4x+1=0$

Use the quadratic equation to solve for $\ x$ .

Remember that the quadratic equation is as follows.

$\\ \\ x=\frac{-b\pm\sqrt{b^2-4\cdot a\cdot c}}{2\cdot a}$ , where a,b and c refer to the coefficents in the

equation ax^2+bx+c=0 .

In this case, a=3 , b=4 , and c=1 .

After plugging in those values, we get

$\\ \\ x=\frac{-4\pm\sqrt{4^2-4\cdot3\cdot1}}{2\cdot3} =\frac{-4 \pm \sqrt{4}}{6}=\frac{-4 \pm 2}{6}$ .

So the critical points values are:

$\\ \\ c_1=\frac{-4+2}{6}=\frac{-1}{3}$

$\\ \\ c_2=\frac{-4-2}{6}=-1$

Report an Error

Example Question #3 : How To Graph Functions Of Points

Find the value(s) of the critical point(s) of

f(x)=5x^3+10x^2+x+100 .

Possible Answers:

$\\ c_1=\frac{-10+\sqrt{85}}{30} \\ \\ c_2=\frac{-10-\sqrt{85}}{30}$

$\\ c_1=\frac{\sqrt{85}}{15} \\ \\ c_2=\frac{-\sqrt{85}}{15}$

$\\ c_1=0 \\ \\ c_2=0$

$\\ c_1=\frac{-10+\sqrt{85}}{15} \\ \\ c_2=\frac{-10-\sqrt{85}}{15}$

$\\ c_1=1 \\ \\ c_2=0$

Correct answer:

$\\ c_1=\frac{-10+\sqrt{85}}{15} \\ \\ c_2=\frac{-10-\sqrt{85}}{15}$

Explanation:

In order to find the critical points, we must find $\ f'(x)$ and solve for $\ x$ .

$\\ \\ f(x)=5x^3+10x^2+x+100$

$\\ \\ f'(x)=15x^2+20x+1$

Set $\ f'(x)=0$

$\\ \\ 15x^2+20x+1=0$

Use the quadratic equation to solve for $\ x$ .

Remember that the quadratic equation is as follows.

$\\ \\ x=\frac{-b\pm\sqrt{b^2-4\cdot a\cdot c}}{2\cdot a}$ , where a,b and c refer to the coefficents in the equation ax^2+bx+c=0 .

In this case, a=15 , b=20 , and c=1 .

After plugging in those values, we get.

${}\\ x=\frac{-20\pm\sqrt{20^2-4\cdot15\cdot1}}{2\cdot15} =\frac{-20 \pm \sqrt{340}}{30} \\ \\ x=\frac{-20 \pm 2\cdot\sqrt{85}}{30}$

So the critical points values are,

${}\\ \\ c_1=\frac{-20+2\cdot \sqrt{85}}{30}=\frac{-10+\sqrt{85}}{15} \\ \\ c_2=\frac{-20-2\cdot \sqrt{85}}{30}=\frac{-10-\sqrt{85}}{15}$

Report an Error

Example Question #2 : How To Graph Functions Of Points

Find the critical points of

f(x)=x^3+3x^2+x+5

Possible Answers:

$\\ c_1=-1+\frac{\sqrt{6}}{3}\\\\\ c_2=-1-\frac{\sqrt{6}}{3}$

The critical points are complex.

$\\ c_1=0\\\\\ c_2=-1-\frac{\sqrt{6}}{3}$

$\\ c_1=\frac{\sqrt{6}}{3}\\\\\ c_2=-\frac{\sqrt{6}}{3}$

Correct answer:

$\\ c_1=-1+\frac{\sqrt{6}}{3}\\\\\ c_2=-1-\frac{\sqrt{6}}{3}$

Explanation:

First we need to find f'(x) .

f(x)=x^3+3x^2+x+5

f'(x)=3x^2+6x+1

Now we set f'(x)=0.

3x^2+6x+4=0.

Now we can use the quadratic equation in order to find the critical points.

Remember that the quadratic equation is

$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$ ,

where a,b,c refer to the coefficients in the equation

ax^2+bx+c=0

In this case, a=3, b=6, and c=1.

$x=\frac{-6\pm\sqrt{(-6)^2-4(3)(1)}}{(2)(3)}$

$x=\frac{-6\pm\sqrt{24}}{6}=\frac{-6\pm2\sqrt{6}}{6}$

Thus are critical points are

$c_1=\frac{-6+2\sqrt{6}}{6}=-1+\frac{\sqrt{6}}{3}$

$c_2=\frac{-6-2\sqrt{6}}{6}=-1-\frac{\sqrt{6}}{3}$

Report an Error

Example Question #5 : Other Points

Find the critical points of

f(x)=x^2-2x+1 .

Possible Answers:

There are no critical points.

x=2

x=1

x=0

Correct answer:

x=1

Explanation:

In order to find the critical points, we need to find f'(x) using the power rule $f(x)=x^n \rightarrow f'(x)=nx^{n-1}$ .

f(x)=x^2-2x+1

f'(x)=2x-2

Now we set f'(x)=0 , and solve for .

2x-2=0

2x=2

x=1

Thus x=1 is a critical point.

Report an Error

Example Question #4 : How To Graph Functions Of Points

Find the critical point(s) of $f(x)=2x^{2}-5x+4$ .

Possible Answers:

$c=\frac{5}{4}$ and $c=-\frac{4}{5}$

$c=\frac{4}{5}$

$c=\frac{5}{4}$ and $c=-\frac{5}{4}$

$c=\frac{5}{4}$

$c=\frac{4}{5}$ and $c=-\frac{4}{5}$

Correct answer:

$c=\frac{5}{4}$

Explanation:

To find the critical point(s) of a function f(x) , take its derivative f'(x) , set it equal to , and solve for .

Given $f(x)=2x^{2}-5x+4$ , use the power rule

$f(x)=x^n \rightarrow f'(x)=nx^{n-1}$ to find the derivative. Thus the derivative is, f'(x)=4x-5=0 .

Since 4x-5=0 :

4x=5

$x=\frac{5}{4}$

The critical point is $c=\frac{5}{4}$ .

Report an Error

Example Question #2 : Other Points

Find the critical points of

f(x)=3x^3-20x^2+4x+99 .

Possible Answers:

x=0

$c=\frac{20-2\sqrt{91}}{9}$

$\\ c_1=\frac{20+2\sqrt{91}}{9} \\ \\ c_2=\frac{20-2\sqrt{91}}{9}$

There are no critical points

$\\ c=\frac{20+2\sqrt{91}}{9}$

Correct answer:

$\\ c_1=\frac{20+2\sqrt{91}}{9} \\ \\ c_2=\frac{20-2\sqrt{91}}{9}$

Explanation:

In order to find the critical points, we must find f'(x) using the power rule $f(x)=x^n \rightarrow f'(x)=nx^{n-1}$ .

f(x)=3x^3-20x^2+4x+99

f'(x)=9x^2-40x+4 .

Now we set f'(x)=0 .

9x^2-40x+4=0

Now we use the quadratic equation in order to solve for .

Remember that the quadratic equation is as follows.

$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$ ,

where a,b,c correspond to the coefficients in the equation

ax^2+bx+c=0 .

In this case, a=9, b=-40, c=4.

$x=\frac{40\pm\sqrt{(-40)^2-4(9)(4)}}{2(9)}$

$x=\frac{40\pm\sqrt{1600-144}}{18}$

$x=\frac{40\pm\sqrt{1456}}{18}=\frac{40\pm4\sqrt{91}}{18}$

Then are critical points are:

$c_1=\frac{40+4\sqrt{91}}{18}=\frac{20+2\sqrt{91}}{9}$

$c_2=\frac{40-4\sqrt{91}}{18}=\frac{20-2\sqrt{91}}{9}$

Report an Error

Example Question #2 : Other Points

Find all the critical points of

f(x)=x^3-2x+10 .

Possible Answers:

x=0

There are no critical points.

$\\ x=\sqrt{\frac{2}{3}} \\ \\ x=-\sqrt{\frac{2}{3}}$

$\\ x=\sqrt{\frac{2}{3}}$

$x=-\sqrt{\frac{2}{3}}$

Correct answer:

$\\ x=\sqrt{\frac{2}{3}} \\ \\ x=-\sqrt{\frac{2}{3}}$

Explanation:

In order to find the critical points, we first need to find f'(x) using the power rule $f(x)=x^n \rightarrow f'(x)=nx^{n-1}$ ..

f(x)=x^3-2x+10

f'(x)=3x^2-2

Now we set f'(x)=0 .

3x^2-2=0

3x^2=2

$x^2=\frac{2}{3}$

$x=\pm\sqrt{\frac{2}{3}}$

Thus the critical points are at

$x=\sqrt{\frac{2}{3}}$ , and

$x=-\sqrt{\frac{2}{3}}$ .

Report an Error

Example Question #2 : Other Points

Find the critical points of the following function:

$y=\frac{x^6}{6}+\frac{3x^5}{5}-\frac{13x^4}{4}-5x^3$

Possible Answers:

$x=\left \{ {-5, -1, 0, 3} \right \}$

$x=\left \{ {0, 1.332, 6.013} \right \}$

$x=\left \{ {{-5, -1, 0, 3}} \right \}$

$x=\left \{ {-3, 0, 1, 5} \right \}$

$x=\left \{ {-6.013, -1.332, 0} \right \}$

Correct answer:

$x=\left \{ {{-5, -1, 0, 3}} \right \}$

Explanation:

To find critical points the derivative of the function must be found.

$y=\frac{x^6}{6}+\frac{3x^5}{5}-\frac{13x^4}{4}-5x^3$

y'=x^5+3x^4-13x^3-15x^3

Critical points occur where the derivative equals zero.

0=x^5+3x^4-13x^3-15x^3

0=x^2(x+1)(x+5)(x-3)

$x=\left \{ {{-5, -1, 0, 3}} \right \}$

Report an Error

Example Question #3 : How To Graph Functions Of Points

Determine the point on the graph that is not changing if $f(x)=x^{2}-12x+32$ .

Possible Answers:

(0,0)

(6,-2)

(0,-4)

(3,-2)

(6,-4)

Correct answer:

(6,-4)

Explanation:

To find the point where the graph of f(x) is not changing, we must set the first derivative equal to zero and solve for .

To evaluate this derivate, we need the following formulae:

$\frac{d}{dx}(c)=0, \frac{d}{dx}(x)=1, \frac{d}{dx}cx=c$

$\frac{d}{dx}(x^{n}))=nx^{n-1}, \frac{d}{dx}(cx^{n})=ncx^{n-1}$

$f'(x)=2x^{2-1}-12x^{1-1}+0=2x-12$

Now, setting the derivate equal to to find where the graph is not changing:

2x-12=0 ==> x=6

Now, to find the corresponding value, we plug this value back into f(x) :

$f(6)=6^{2}-12(6)+32=36-72+32=-4$

Therefore, the point where f(x) is not changing is (6,-4)

Report an Error

View Calculus Tutors

Abhisek
Certified Tutor

University of Florida, Bachelor of Engineering, Computer Science.

View Calculus Tutors

Magdy
Certified Tutor

Cairo University, Egypt, Bachelor of Science, Electrical Engineering. New Mexico State University-Main Campus, Doctor of Phil...

View Calculus Tutors

Yuliya
Certified Tutor

University of Maryland-College Park, Bachelor of Science, Mathematics. George Washington University, Masters in Education, Ed...

All Calculus 1 Resources

10 Diagnostic Tests 438 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Atlanta, Physics Tutors in Philadelphia, Physics Tutors in Boston, SSAT Tutors in New York City, English Tutors in Phoenix, Algebra Tutors in Philadelphia, SSAT Tutors in Boston, English Tutors in Boston, SSAT Tutors in Dallas Fort Worth, Spanish Tutors in Chicago

Popular Courses & Classes

Spanish Courses & Classes in Boston, GRE Courses & Classes in Los Angeles, ISEE Courses & Classes in Philadelphia, GRE Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Boston, LSAT Courses & Classes in Washington DC, GRE Courses & Classes in Atlanta, GRE Courses & Classes in Phoenix, MCAT Courses & Classes in Phoenix, GMAT Courses & Classes in Dallas Fort Worth

Popular Test Prep

MCAT Test Prep in New York City, GMAT Test Prep in San Francisco-Bay Area, GMAT Test Prep in Dallas Fort Worth, GRE Test Prep in Washington DC, GRE Test Prep in Phoenix, SAT Test Prep in Seattle, SSAT Test Prep in San Diego, ACT Test Prep in Philadelphia, ISEE Test Prep in Phoenix, SSAT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Calculus 1 : How to graph functions of points

Study concepts, example questions & explanations for Calculus 1

All Calculus 1 Resources

Example Questions

Example Question #1 : How To Graph Functions Of Points

Example Question #2 : How To Graph Functions Of Points

Example Question #3 : How To Graph Functions Of Points

Example Question #2 : How To Graph Functions Of Points

Example Question #5 : Other Points

Example Question #4 : How To Graph Functions Of Points

Example Question #2 : Other Points

Example Question #2 : Other Points

Example Question #2 : Other Points

Example Question #3 : How To Graph Functions Of Points

All Calculus 1 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: