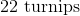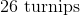All Common Core: 6th Grade Math Resources
Example Questions
Example Question #54 : Equations
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Example Question #55 : Equations
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Example Question #1 : Solve Unit Rate Problems: Ccss.Math.Content.6.Rp.A.3b
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Example Question #2 : Solve Unit Rate Problems: Ccss.Math.Content.6.Rp.A.3b
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Example Question #3 : Solve Unit Rate Problems: Ccss.Math.Content.6.Rp.A.3b
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Example Question #71 : How To Find A Ratio
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Example Question #72 : How To Find A Ratio
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Example Question #73 : How To Find A Ratio
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Example Question #74 : How To Find A Ratio
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Example Question #75 : How To Find A Ratio
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
All Common Core: 6th Grade Math Resources