Intermediate Geometry : How to find the length of the side of of an acute / obtuse isosceles triangle
Study concepts, example questions & explanations for Intermediate Geometry
All Intermediate Geometry Resources
Example Questions
Example Question #1 : How To Find The Length Of The Side Of Of An Acute / Obtuse Isosceles Triangle
Find the perimeter of the triangle below.
Use the Pythagorean Theorem to find the base of the right triangle.
Now, because two of the angles in this triangle are the same, this is an isosceles triangle. In an isosceles triangle, the sides that are directly across from the congruent angles are also congruent.
In addition, the height in an isosceles triangle will always cut the 3rd side in half. With this information, fill out the triangle as shown below:
To find the perimeter, add up all the sides.
Example Question #2 : How To Find The Length Of The Side Of Of An Acute / Obtuse Isosceles Triangle
Find the perimeter of the triangle below.
Use the Pythagorean Theorem to find the base of the right triangle.
Now, because two of the angles in this triangle are the same, this is an isosceles triangle. In an isosceles triangle, the sides that are directly across from the congruent angles are also congruent.
In addition, the height in an isosceles triangle will always cut the 3rd side in half. With this information, fill out the triangle as shown below:
To find the perimeter, add up all the sides.
Example Question #2 : How To Find The Length Of The Side Of Of An Acute / Obtuse Isosceles Triangle
A triangle has sides of lengths 14, 18, and 20. Is the triangle scalene or isosceles?
Scalene
Isosceles
Scalene
A triangle with three sides of different length is, by definition, scalene.
Example Question #3 : How To Find The Length Of The Side Of Of An Acute / Obtuse Isosceles Triangle
Given: Regular Pentagon 
True or false: 
False
True
True
Below is regular Pentagon 
By symmetry, all of the radii of a regular pentagon are congruent - specifically, 
Example Question #52 : Acute / Obtuse Isosceles Triangles
If a triangle has side lengths of 
The triangle inequality theorem states that the sum of the lengths of any two sides must be greater than the length of the third side. The relationship can be represented by the following inequalities:
The side length of 
Example Question #53 : Acute / Obtuse Isosceles Triangles
If a triangle has side lengths of 
The triangle inequality theorem states that the sum of the lengths of any two sides must be greater than the length of the third side. The relationship can be represented by the following inequalities:
The side length of 
Example Question #6 : How To Find The Length Of The Side Of Of An Acute / Obtuse Isosceles Triangle
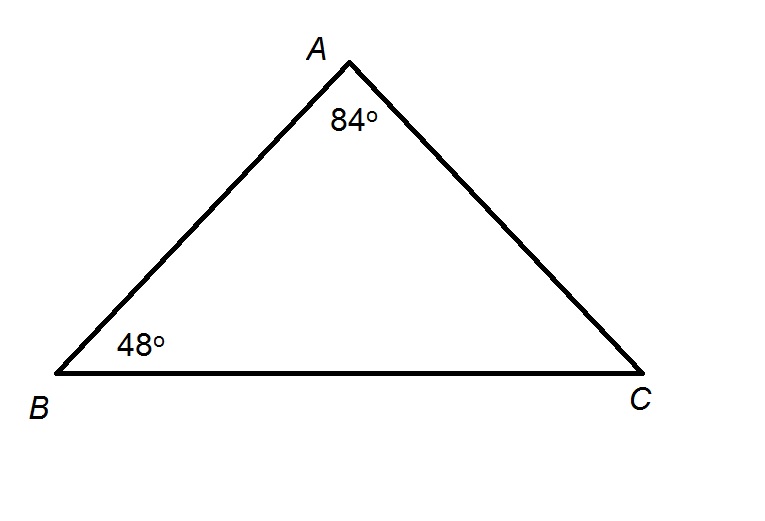
Figure NOT drawn to scale.
Refer to the above diagram.
True or false: 
True
False
True
The sum of the measures of the interior angles of a triangle is 
Substitute the given two angle measures and solve for 
Subtract 
Example Question #1 : How To Find The Length Of The Side Of Of An Acute / Obtuse Isosceles Triangle
Refer to the above triangle. By what statement does it follow that 
The Hinge Theorem
The Angle-Angle Postulate
The Angle-Side-Angle Postulate
The Converse of the Isosceles Triangle Theorem
The Converse of the Pythagorean Theorem
The Converse of the Isosceles Triangle Theorem
We are given that, in 
Example Question #2 : How To Find The Length Of The Side Of Of An Acute / Obtuse Isosceles Triangle
Given 
It cannot be determined from the information given.
Having three sides of different lengths, this triangle is scalene. In any scalene triangle, the angle with greatest measure is opposite the longest side, and the angle with least measure is opposite the shortest side. Therefore, since 
All Intermediate Geometry Resources
