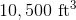Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math I : 3-Dimensional Geometry

Study concepts, example questions & explanations for SAT II Math I

Create An Account

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Volume

A circular swimming pool has diameter meters and depth 2 meters throughout. Which of the following expressions give the amount of water it holds, in cubic meters?

Possible Answers:

$\frac{ \pi k^{2}} {4}$

$4\pi k$

$2\pi k^{2}$

$\frac{ \pi k^{2}} {2}$

$2\pi k$

Correct answer:

$\frac{ \pi k^{2}} {2}$

Explanation:

The pool can be seen as a cylinder with diameter - and, subsequently, radius half this, or $\frac{k}{2}$ - and depth, or height, 2. The volume of a cylinder is defined by the formula

$V = \pi r^{2} h = \pi \left ( \frac{k}{2} \right ) ^{2} \cdot 2 = \pi \cdot \frac{k^{2}} {4} \right )\cdot 2 = \frac{ \pi k^{2}} {2}$

Report an Error

Example Question #1 : Volume

Swimming_pool

The above depicts a rectangular swimming pool for an apartment. 60% of the pool is six feet deep, and the remaining part of the pool is four feet deep. How many cubic feet of water does the pool hold?

Possible Answers:

$8,750 \textrm{ ft} ^{3}$

$9,750 \textrm{ ft} ^{3}$

$7,000 \textrm{ ft} ^{3}$

None of the other choices gives the correct answer.

$10,500\textrm{ ft} ^{3}$

Correct answer:

None of the other choices gives the correct answer.

Explanation:

The cross-section of the pool is the area of its surface, which is the product of its length and its width:

$50 \times 35 = 1,750$ square feet.

Since 60% of the pool is six feet deep, this portion of the pool holds

$0.60 \times 1,750 \times 6 = 6,300$ cubic feet of water.

Since the remainder of the pool - 40% - is four feet deep, this portion of the pool holds

$0.4 \times 1,750 \times 4 = 2,800$ cubic feet of water.

Add them together: the pool holds

6,300 + 2,800 = 9,100 cubic feet of water.

This answer is not among the choices.

Report an Error

Example Question #1 : Volume

Find the volume of a cube in inches with a side of $1.5 \textup{ feet}.$

Possible Answers:

$40.5 \textup{ inches}^3$

$0.001953 \textup{ inches}^3$

$5832 \textup{ inches}^3$

$13458 \textup{ inches}^3$

$54 \textup{ inches}^3$

Correct answer:

$5832 \textup{ inches}^3$

Explanation:

Convert the side dimension to inches first before finding the volume.

$1.5 \textup{ feet} \times \left(\frac{12 \textup{ inches}}{1 \textup{ feet}}\right)= 18 \textup{ inches}$

Write the volume for a cube and substitute the new side to obtain the volume in inches.

$V=s^3 =(18 \textup{ inches})^3 = 5832 \textup{ inches}^3$

Report an Error

Example Question #1 : 3 Dimensional Geometry

Example cylinder

Figure not drawn to scale.

What is the volume of the cylinder above?

Possible Answers:

52.36 in³

48.79 in³

66.13 in³

56.55 in³

94.25 in³

Correct answer:

56.55 in³

Explanation:

In order to find the volume of a cylinder, you find the area of the circular top and multiply it by the height.

Example cylinder

$\small \small Volume=\pi r{^{2}}h$

$\small \pi (3{^{2}})(2)=\pi(9)(2)=18\pi=56.55$

The volume of the cylinder is 56.55 in³

Report an Error

Example Question #1 : Volume

Cone example

Figure not drawn to scale

If the volume of the cone above is 47.12 ft³, what is the radius of the base?

Possible Answers:

5 ft

2 ft

3 ft

4 ft

3.5ft

Correct answer:

3 ft

Explanation:

Because we have been given the volume of the cone and have been asked to find the radius of the base of the cone, we must work backwards using the volume formula.

Cone example

$\small Volume= {\frac{1}{3}}\pi r{^{2}}h$

$\small \small 47.12={\frac{1}{3}}\pi r{^{2}}(5)={\frac{5}{3}}\pi r{^{2}}$

$\small \left({\frac{3}{5}} \right)47.12=\left({\frac{3}{5}} \right )\left({\frac{5}{3}} \right )\pi r{^{2}}$

$\small \frac{28.27}{\pi}=r{^{2}}$

$\small 9.00=r{^{2}}$

$\small r=3$

The radius of the base of the cone is 3 ft.

Report an Error

Example Question #1 : Volume

Box example

Figure not drawn to scale.

What is the volume of the above image?

Possible Answers:

64 yd³

42 yd²

42 yd³

32 yd³

84 yd²

Correct answer:

42 yd³

Explanation:

You can find the volume of a box by following the equation below:

$\small Volume=(length)(height)(depth)$

$\small (7)(3)(2)=42$

The surface area of the box is 42 yd³(remember that volume measurements are cubic units NOT square units)

Report an Error

Example Question #1 : Volume

What is the volume of the following tetrahedron? Assume the figure is a regular tetrahedron.

Possible Answers:

$\4\sqrt{3}m^3$

$\frac{2\sqrt{2}}{3}m^3$

$\frac{\sqrt{2}}{3}m^3$

$\frac{3\sqrt{2}}{2}m^3$

$\frac{8\sqrt{2}}{3}m^3$

Correct answer:

$\frac{2\sqrt{2}}{3}m^3$

Explanation:

A regular tetrahedron is composed of four equilateral triangles. The formula for the volume of a regular tetrahedron is:

$V=\frac{a^3\sqrt{2}}{12}$ , where represents the length of the side.

Plugging in our values we get:

$V=\frac{(2\: m)^3\sqrt{2}}{12}$

$V=\frac{8\: m^3\sqrt{2}}{12} = \frac{2\sqrt{2}}{3}m^3$

Report an Error

Example Question #2 : Volume

Find the volume of a tetrahedron with an edge of $1\:cm$ .

Possible Answers:

$3\:cm^3$

$6\sqrt{2}\:cm^3$

$\frac{\sqrt2}{12}\:cm^3$

$\frac{1}{6}\:cm^3$

$\frac{\sqrt3}{4}\:cm^3$

Correct answer:

$\frac{\sqrt2}{12}\:cm^3$

Explanation:

Write the formula for the volume of a tetrahedron.

$V=\frac{s^3}{6\sqrt 2}$

Substitute in the length of the edge provided in the problem.

$V=\frac{(1\:cm)^3}{6\sqrt2}=\frac{1}{6\sqrt2}\:cm^3$

Rationalize the denominator.

$V= \frac{1}{6\sqrt2}\:cm\cdot \frac{\sqrt2}{\sqrt2} = \frac{\sqrt2}{12}\:cm^3$

Report an Error

Example Question #1 : How To Find The Volume Of A Tetrahedron

Find the volume of a tetrahedron with an edge of $\sqrt2\:in$ .

Possible Answers:

$\frac{1}{6}\:in^3$

$\sqrt3\:in^3$

$\frac{1}{2}\:in^3$

$\frac{2}{3}\:in^3$

$\frac{1}{3}\:in^3$

Correct answer:

$\frac{1}{3}\:in^3$

Explanation:

Write the formula for the volume of a tetrahedron.

$V=\frac{s^3}{6\sqrt 2}$

Substitute in the length of the edge provided in the problem:

$V=\frac{(\sqrt2\:in)^3}{6\sqrt2}$

Cancel out the $\sqrt2$ in the denominator with one in the numerator:

$V= \frac{(\sqrt2)^3}{6\sqrt2}\:in^3$

A square root is being raised to the power of two in the numerator; these two operations cancel each other out. After canceling those operations, reduce the remaining fraction to arrive at the correct answer:

$V= \frac{(\sqrt2)^2}{6}\:in^3=\frac{2}{6}\:in^3=\frac{1}{3}\:in^3$

Report an Error

Example Question #2 : How To Find The Volume Of A Tetrahedron

Find the volume of a tetrahedron with an edge of $6\:cm$ .

Possible Answers:

$36\sqrt2\:cm^3$

$18\sqrt2\:cm^3$

Correct answer:

$18\sqrt2\:cm^3$

Explanation:

Write the formula for finding the volume of a tetrahedron.

$V=\frac{s^3}{6\sqrt 2}$

Substitute in the edge length provided in the problem.

$V=\frac{(6\:cm)^3}{6\sqrt 2}=\frac{6^3}{6\sqrt 2}\:cm^3$

Cancel out the in the denominator with part of the 6^3 in the numerator:

$V= \frac{6^2}{\sqrt2}\:cm^3$

Expand, rationalize the denominator, and reduce to arrive at the correct answer:

$V= \frac{36}{\sqrt2}\:cm^3=\frac{36}{\sqrt2}\:cm^3 \cdot \frac{\sqrt2}{\sqrt2} =\frac{36\sqrt2}{2}\:cm^3 = 18\sqrt2\:cm^3$

Report an Error

View SAT Subject Test in Mathematics Level 1 Tutors

Tarvinder
Certified Tutor

University of Arkansas - Monticello, Bachelor of Science, Mathematics. Tulane University of Louisiana, Master of Science, Com...

View SAT Subject Test in Mathematics Level 1 Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

View SAT Subject Test in Mathematics Level 1 Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

LSAT Tutors in Seattle, MCAT Tutors in Chicago, French Tutors in San Francisco-Bay Area, Math Tutors in Philadelphia, Algebra Tutors in Boston, English Tutors in Seattle, English Tutors in San Diego, ACT Tutors in Los Angeles, French Tutors in Dallas Fort Worth, Biology Tutors in Los Angeles

Popular Courses & Classes

Spanish Courses & Classes in Philadelphia, MCAT Courses & Classes in Washington DC, SAT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Denver, SAT Courses & Classes in Miami, GMAT Courses & Classes in Los Angeles, ISEE Courses & Classes in Atlanta, MCAT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Philadelphia, ACT Courses & Classes in Los Angeles

Popular Test Prep

LSAT Test Prep in Washington DC, ACT Test Prep in Los Angeles, LSAT Test Prep in Atlanta, GMAT Test Prep in Chicago, GRE Test Prep in Boston, MCAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Chicago, GMAT Test Prep in Boston, SSAT Test Prep in Dallas Fort Worth, GMAT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math I : 3-Dimensional Geometry

Study concepts, example questions & explanations for SAT II Math I

All SAT II Math I Resources

Example Questions

Example Question #1 : Volume

Example Question #1 : Volume

Example Question #1 : Volume

Example Question #1 : 3 Dimensional Geometry

The volume of the cylinder is 56.55 in³

Example Question #1 : Volume

If the volume of the cone above is 47.12 ft³, what is the radius of the base?

The radius of the base of the cone is 3 ft.

Example Question #1 : Volume

The surface area of the box is 42 yd³(remember that volume measurements are cubic units NOT square units)

Example Question #1 : Volume

Example Question #2 : Volume

Example Question #1 : How To Find The Volume Of A Tetrahedron

Example Question #2 : How To Find The Volume Of A Tetrahedron

All SAT II Math I Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback:

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math I : 3-Dimensional Geometry

Study concepts, example questions & explanations for SAT II Math I

All SAT II Math I Resources

Example Questions

Example Question #1 : Volume

Example Question #1 : Volume

Example Question #1 : Volume

Example Question #1 : 3 Dimensional Geometry

The volume of the cylinder is 56.55 in3

Example Question #1 : Volume

If the volume of the cone above is 47.12 ft3, what is the radius of the base?

The radius of the base of the cone is 3 ft.

Example Question #1 : Volume

The surface area of the box is 42 yd3 (remember that volume measurements are cubic units NOT square units)

Example Question #1 : Volume

Example Question #2 : Volume

Example Question #1 : How To Find The Volume Of A Tetrahedron

Example Question #2 : How To Find The Volume Of A Tetrahedron

All SAT II Math I Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

The volume of the cylinder is 56.55 in³

If the volume of the cone above is 47.12 ft³, what is the radius of the base?

The surface area of the box is 42 yd³(remember that volume measurements are cubic units NOT square units)