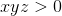First multiply the fraction in the numerator.

$\displaystyle \dpi{100} \frac{1}{2}\times \frac{1}{3}=\frac{1\times 1}{2\times 3}=\frac{1}{6}$

Now we have $\displaystyle \dpi{100} \frac{\frac{1}{6}}{\frac{1}{9}}$

Never divide fractions.  We multiply the numerator by the reciprocal of the denominator.

$\displaystyle \dpi{100} \frac{\frac{1}{6}}{\frac{1}{9}}=\frac{1}{6}\div \frac{1}{9}=\frac{1}{6}\times \frac{9}{1}=\frac{1\times 9}{6\times 1}=\frac{9}{6}=\frac{3}{2}$

The easiest way to see that all four are equivalent is to convert each to a decimal product, noting that twenty percent and one-fifth are equal to $\displaystyle 0.2$, and twenty-five percent and one fourth are equal to $\displaystyle 0.25$.

One fourth of 0.2: $\displaystyle \frac{1}{4}*0.2=\frac{1}{4}*\frac{2}{10}=\frac{2}{40}=\frac{1}{20}$

One fifth of 0.25: $\displaystyle \frac{1}{5}*0.25=\frac{1}{5}*\frac{25}{100}=\frac{25}{500}=\frac{5}{100}=\frac{1}{20}$

Twenty-five percent of one fifth: $\displaystyle *\frac{1}{5}=\frac{25}{100}*\frac{1}{5}=\frac{25}{500}=\frac{1}{20}$

Twenty percent of one fourth: $\displaystyle *\frac{1}{4}=\frac{20}{100}*\frac{1}{4}=\frac{20}{400}=\frac{1}{20}$

The answer is $\displaystyle 7.341\times10^{^{-3}}$. 

When three negative numbers are multiplied together, the product will be negative as well. All the other expressions are true.

The problem is asking for a number whose product with 5 yields a number congruent to 3 in modulo 6 arithmetic - that is, a number which, when divided by 6, yields remainder 3. We multiply 5 by each choice and look for a product with this characteristic.

$\displaystyle 5 \times 1 = 5$; $\displaystyle 5 \div 6 = 0 \textrm{ R } 5$

$\displaystyle 5 \times 2 = 10$; $\displaystyle 10 \div 6 = 1 \textrm{ R } 4$

$\displaystyle 5 \times 3= 15$; $\displaystyle 15 \div 6 = 2 \textrm{ R } 3$

$\displaystyle 5 \times 4=20$; $\displaystyle 20 \div 6 = 3 \textrm{ R } 2$

$\displaystyle 5 \times 5 = 25$; $\displaystyle 25 \div 6 = 4 \textrm{ R } 1$

The only choice whose product with 5 yields a number congruent to 3 modulo 6 is 3, so this is the correct choice.

The problem is asking for a number whose cube is a number congruent to 9 in modulo 10 arithmetic - that is, a number whose cube, when divided by 10, yields remainder 9. If the quotient of a number and 10 has remainder 9, then it is an integer that ends with the digit "9". Since this makes the cube odd, the number that is cubed must also be odd, so we need only test the five odd integers:

$\displaystyle 1 ^{3} = 1$

$\displaystyle 3^{3}= 27$

$\displaystyle 5^{3} = 125$

$\displaystyle 7 ^{3} = 343$

$\displaystyle 9^{3} = 729$

Only 9 fits the criterion, so "one" is the correct response.

The problem is asking for a number whose square is a number congruent to 1 in modulo 12 arithmetic - that is, a number whose square, when divided by 12, yields remainder 1. This square must be odd, so the number squared must also be odd. Therefore, we need only test the odd integers. We see that:

$\displaystyle 1^{2} = 1 ; 1 \div 12 = 0 \textrm{ R }1$

$\displaystyle 3^{2} = 9 ; 9 \div 12 = 0 \textrm{ R }9$

$\displaystyle 5^{2} = 25 ; 25 \div 12 = 2 \textrm{ R }1$

$\displaystyle 7^{2} =49 ; 49 \div 12 = 4 \textrm{ R }1$

$\displaystyle 9^{2} = 81 ; 81 \div 12 = 8 \textrm{ R }9$

$\displaystyle 11^{2} = 121; 121 \div 12 = 10 \textrm{ R }1$

Four of the integers have squares congruent to 1 in modulo 12 arithmetic.

We can write 2 pounds, 5 ounces as just ounces as follows:

$\displaystyle 2 \textrm{ lbs } 5 \textrm{ oz } =\left ( 2 \times 16 + 5 \right ) \textrm{ oz } = 37 \textrm{ oz }$

Multiply:

$\displaystyle 6 \times 2 \textrm{ lbs } 5 \textrm{ oz }$

$\displaystyle = 6 \times 37 \textrm{ oz }$

$\displaystyle = 222 \textrm{ oz }$

Divide by 16, noting quotient and remainder, to get pounds and ounces:

$\displaystyle 222 \div 16 = 13 \textrm{ R } 14$

Therefore, the correct response is 13 pounds, 14 ounces.

The problem is asking for a number whose product with 6 yields a number congruent to 5 in modulo 12 arithmetic - that is, a number which, when divided by 12, yields remainder 6. 

However, 6 multiplied by any odd number yields a number which, when divided by 12, yields remainder 6, as is demonstrated using our choices:

$\displaystyle 6 \times 3 = 18 ; 18 \div 12 = 1 \textrm{ R }6$

$\displaystyle 6 \times 5 = 6 ; 30 \div 12 = 2 \textrm{ R }6$

$\displaystyle 6 \times 7 = 42 ; 42 \div 12 = 3 \textrm{ R }6$

$\displaystyle 6 \times 9 = 54 ; 54 \div 12 = 4 \textrm{ R }6$

Each of the choices yields a product congruent to 6 modulo 12, so none of them is a correct choice.

Scientific notation is used to simplify exceptionally complex numbers and to quickly present the number of significant figures in a given value. The value is converted to an exponent form using base ten, such that only a single-digit term with any given number of decimal places is used to represent the significant figures of the given value. Non-significant zeroes can be omitted from the leading term, and represented only in the base ten exponent.

The given number has three significant figure ($\displaystyle 932$) so we write out number as $\displaystyle 9.32$

You must move the decimal place two places to the right, or in other words multiply by $\displaystyle 100$. When you move the decimal place to the right, you multiply the number by $\displaystyle 10^{-2}$, so it is $\displaystyle 9.32\times10^{-2}$.