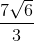ACT Math : How to add square roots
Study concepts, example questions & explanations for ACT Math
All ACT Math Resources
Example Questions
Example Question #1 : How To Add Square Roots
Find the sum:
Find the Sum:
Simplify the radicals:
Example Question #11 : Square Roots And Operations
Add
The first step when adding square roots is to simplify each term as much as possible. Since the first term has a square within the square root, we can reduce 
Only terms that have the same expression within the sqaure root can be combined. In this question, these are the first and third terms. When combining terms, the expression within the square root stays the say, while the terms out front are added. Therefore we get 
Example Question #91 : Arithmetic
Simplify:
None of the other answers
Take each fraction separately first:
(2√3)/(√2) = [(2√3)/(√2)] * [(√2)/(√2)] = (2 * √3 * √2)/(√2 * √2) = (2 * √6)/2 = √6
Similarly:
(4√2)/(√3) = [(4√2)/(√3)] * [(√3)/(√3)] = (4√6)/3 = (4/3)√6
Now, add them together:
√6 + (4/3)√6 = (3/3)√6 + (4/3)√6 = (7/3)√6
Example Question #3 : Square Roots And Operations
Simplify the following expression:
Begin by factoring out each of the radicals:
For the first two radicals, you can factor out a 
The other root values cannot be simply broken down. Now, combine the factors with 
This is your simplest form.
Example Question #4 : Square Roots And Operations
Solve for 
Note, 
Begin by getting your 
Next, you can combine your radicals. You do this merely by subtracting their respective coefficients:
Now, square both sides:
Solve by dividing both sides by 
Example Question #12 : Square Roots And Operations
Simplify:
Begin simplifying by breaking apart the square roots in question. Thus, you know:
Now, with square roots, you can combine factors just as if a given root were a variable. So, just as 
Example Question #13 : Square Roots And Operations
Simplify: 
Begin simplifying by breaking apart the square roots in question. Thus, you know:
Now, with square roots, you can combine factors just as if a given root were a variable. So, just as 
All ACT Math Resources
