All Pre-Algebra Resources
Example Questions
Example Question #1 : Volume Of A Rectangular Solid
Trayvon ordered a new calculator online for his Pre-Algebra class. When it arrived in the mail, he noticed something interesting about the rectangular box it was shipped in. The width of the box was twice the height, and the length of the box was three times the width. If the box was four inches tall, what was the volume of the box?
If the box is 4 inches tall, then its height is 4in. Since the width is twice the height, the width must be 8 inches. Since the length is three times the width, the length must be 24 inches. Since a rectangular box is just a rectangular solid, the formula for the volume of a rectangular solid will give us the volume of the Trayvon's box.




Since the unit of each of our dimensions was inches, our volume will be in cubic inches. Thus our answer is
Example Question #1931 : Hspt Mathematics
A rectangular prism has length 24 inches, width 18 inches, and height 15 inches. Give its volume in cubic feet.
Divide each dimension in inches by 12 to convert from inches to feet:



Multiply the three to get the volume:

Example Question #2 : Volume Of A Rectangular Solid
A rectangular box has a length of 2 meters, a width of 0.5 meters, and a height of 3.2 meters. How many cubes with a volume of one cubic centimeter could fit into this rectangular box?
3,2 x 103
3.2 x 10-3
3.2 x 102
3.2 x 106
3.2
3.2 x 106
In order to figure out how many cubic centimeters can fit into the box, we need to figure out the volume of the box in terms of cubic centimeters. However, the measurements of the box are given in meters. Therefore, we need to convert these measurements to centimeters and then determine the volume of the box.
There are 100 centimeters in one meter. This means that in order to convert from meters to centimeters, we must multiply by 100.
The length of the box is 2 meters, which is equal to 2 x 100, or 200, centimeters.
The width of the box is 0.5(100) = 50 centimeters.
The height of the box is 3.2(100) = 320 centimeters.
Now that all of our measurements are in centimeters, we can calculate the volume of the box in cubic centimeters. Remember that the volume of a rectangular box (or prism) is equal to the product of the length, width, and height.
V = length x width x height
V = (200 cm)(50 cm)(320 cm) = 3,200,000 cm3
To rewrite this in scientific notation, we must move the decimal six places to the left.
V = 3.2 x 106 cm3
The answer is 3.2 x 106.
Example Question #101 : Geometry
If a cube is 
Not enough information provided.
To find the volume of a cube, we multiply length by width by height, which can be represented with the forumla 

Example Question #102 : Geometry
What is the volume of a cube with a side length equal to 
The volume of a a cube (or rectangular prism) can be solved using the following equation:
Example Question #61 : Volume
The volume of a cube is 
Let 
Example Question #51 : Volume Of A Three Dimensional Figure
A given rectangular prism has a length of 


The volume of a given prism 



Substituting in our known values:
Example Question #51 : Volume Of A Three Dimensional Figure
A given rectangular prism has a length of 


The volume 



Example Question #52 : Volume Of A Three Dimensional Figure
A given rectangular prism has a length of 


The volume 



Example Question #1 : Volume Of A Rectangular Solid
The length, width, and height of box is 
Write the formula to find the volume of a rectangular solid.
Substitute the dimensions.
Certified Tutor
Certified Tutor
All Pre-Algebra Resources

















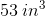
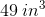










![\sqrt[3]{x^3}=\sqrt[3]{64}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/167958/gif.latex)








































