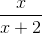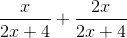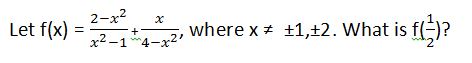Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Expressions

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #31 : Expressions

Simplify the expression.

$\frac{x}{2x+4}+\frac{x}{x+2}$

Possible Answers:

$\frac{x+1}{2x+4}$

$\frac{2x}{3x+6}$

$\frac{x}{x+2}$

$\frac{1}{2x+4}$

$\frac{3x}{2x+4}$

Correct answer:

$\frac{3x}{2x+4}$

Explanation:

To add rational expressions, first find the least common denominator. Because the denominator of the first fraction factors to 2(x+2), it is clear that this is the common denominator. Therefore, multiply the numerator and denominator of the second fraction by 2.

$\frac{x}{2x+4}+\frac{x}{x+2}$

$\frac{x}{2x+4}+\frac{(2)x}{(2)(x+2)}$

$\frac{x}{2x+4}+\frac{2x}{2x+4}$

$\frac{3x}{2x+4}$

This is the most simplified version of the rational expression.

Report an Error

Example Question #32 : Expressions

Simplify the following:

$\frac{x+3}{x-2}+\frac{x-2}{x+3}$

Possible Answers:

$\frac{(x+3)^2+(x-2)^2}{(x+3)(x-2)}$

2x^2-4x+4

$\frac{2(x+3)(x-2)}{(x+3)(x-2)}$

Correct answer:

$\frac{(x+3)^2+(x-2)^2}{(x+3)(x-2)}$

Explanation:

To simplify the following, a common denominator must be achieved. In this case, the first term must be multiplied by (x+2) in both the numerator and denominator and likewise with the second term with (x-3).

$\frac{(x+3)(x+3)}{(x-2)(x+3)}+\frac{(x-2)(x-2)}{(x+3)(x-2)}$

$\frac{(x+3)^2+(x-2)^2}{(x+3)(x-2)}$

Report an Error

Example Question #1 : How To Evaluate Rational Expressions

If √(ab) = 8, and a²= b, what is a?

Possible Answers:

Correct answer:

Explanation:

If we plug in a² for b in the radical expression, we get √(a³) = 8. This can be rewritten as a^3/2 = 8. Thus, log_a8 = 3/2. Plugging in the answer choices gives 4 as the correct answer.

Report an Error

Example Question #2 : How To Evaluate Rational Expressions

Function_part1

Possible Answers:

37/15

–11/5

–37/15

9/5

–9/5

Correct answer:

–11/5

Explanation:

Fraction_part2

Fraction_part3

Report an Error

Example Question #3 : How To Evaluate Rational Expressions

If Jill walks $100\:\text{ft}$ in $20\:\sec$ , how long will it take Jill to walk $1500\:\text{ft}$ ?

Possible Answers:

$400\sec$

$200\sec$

$300\sec$

$30\sec$

$100\sec$

Correct answer:

$300\sec$

Explanation:

To solve this, we need to set a proportion.

$\frac{100\:\text{ft}}{20\sec}=\frac{1500\:\text{ft}}{x}$

Cross Multiply

$100\cdot x=1500\cdot 20$

$x=\frac{30000}{100}=300$

So it will take Jill $300 \sec$ to walk $1500\: \text{ft}$

Report an Error

Example Question #4 : How To Evaluate Rational Expressions

If $\frac{b+c}{c}=\frac{14}{15}$ , then which of the following must be also true?

Possible Answers:

$\frac{b}{c}=\frac{7}{10}$

$\frac{b}{c}=1$

$\frac{b}{c}=-\frac{1}{15}$

$\frac{b}{c}=10$

Correct answer:

$\frac{b}{c}=-\frac{1}{15}$

Explanation:

$\frac{b+c}{c}=\frac{14}{15}$

$\frac{b}{c}+\frac{c}{c}=\frac{14}{15}$

$\frac{b}{c}+1=\frac{14}{15}$

$\frac{b}{c}+1\ {\color{Red} -1}=\frac{14}{15}\ {\color{Red} -1}$

$\frac{b}{c}=\frac{14}{15}-\frac{15}{15}$

$\frac{b}{c}=-\frac{1}{15}$

Report an Error

Example Question #13 : Expressions

Which of the following is equivalent to $\dpi{100} \frac{(\frac{1}{t}-\frac{1}{x})}{x-t}$ ? Assume that denominators are always nonzero.

Possible Answers:

$(xt)^{-1}$

$x^{2}-t^{2}$

$\frac{x}{t}$

$x-t$

$t-x$

Correct answer:

$(xt)^{-1}$

Explanation:

We will need to simplify the expression $\frac{(\frac{1}{t}-\frac{1}{x})}{x-t}$ . We can think of this as a large fraction with a numerator of $\frac{1}{t}-\frac{1}{x}$ and a denominator of $\dpi{100} x-t$ .

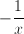
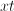
In order to simplify the numerator, we will need to combine the two fractions. When adding or subtracting fractions, we must have a common denominator. $\frac{1}{t}$ has a denominator of $\dpi{100} t$ , and $\dpi{100} -\frac{1}{x}$ has a denominator of $\dpi{100} x$ . The least common denominator that these two fractions have in common is $\dpi{100} xt$ . Thus, we are going to write equivalent fractions with denominators of $\dpi{100} xt$ .

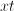
In order to convert the fraction $\dpi{100} \frac{1}{t}$ to a denominator with $\dpi{100} xt$ , we will need to multiply the top and bottom by $\dpi{100} x$ .

$\frac{1}{t}=\frac{1\cdot x}{t\cdot x}=\frac{x}{xt}$

Similarly, we will multiply the top and bottom of $\dpi{100} -\frac{1}{x}$ by $\dpi{100} t$ .

$\frac{1}{x}=\frac{1\cdot t}{x\cdot t}=\frac{t}{xt}$

We can now rewrite $\frac{1}{t}-\frac{1}{x}$ as follows:

$\frac{1}{t}-\frac{1}{x}$ = $\frac{x}{xt}-\frac{t}{xt}=\frac{x-t}{xt}$

Let's go back to the original fraction $\frac{(\frac{1}{t}-\frac{1}{x})}{x-t}$ . We will now rewrite the numerator:

$\frac{(\frac{1}{t}-\frac{1}{x})}{x-t}$ = $\frac{\frac{x-t}{xt}}{x-t}$

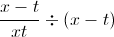
To simplify this further, we can think of $\frac{\frac{x-t}{xt}}{x-t}$ as the same as $\frac{x-t}{xt}\div (x-t)$ . When we divide a fraction by another quantity, this is the same as multiplying the fraction by the reciprocal of that quantity. In other words, $a\div b=a\cdot \frac{1}{b}$ .

$\frac{x-t}{xt}\div (x-t)$ = $\frac{x-t}{xt}\cdot \frac{1}{x-t}$ $=\frac{x-t}{xt(x-t)}$ $= \frac{1}{xt}$

Lastly, we will use the property of exponents which states that, in general, $\frac{1}{a}=a^{-1}$ .

$\frac{1}{xt}=(xt)^{-1}$

The answer is $(xt)^{-1}$ .

Report an Error

Example Question #311 : Algebra

Simplify (4x)/(x²– 4) * (x + 2)/(x²– 2x)

Possible Answers:

x/(x + 2)

x/(x – 2)²

4/(x – 2)²

4/(x + 2)²

(4x²+ 8x)/(x⁴+ 8x)

Correct answer:

4/(x – 2)²

Explanation:

Factor first. The numerators will not factor, but the first denominator factors to (x – 2)(x + 2) and the second denomintaor factors to x(x – 2). Multiplying fractions does not require common denominators, so now look for common factors to divide out. There is a factor of x and a factor of (x + 2) that both divide out, leaving 4 in the numerator and two factors of (x – 2) in the denominator.

Report an Error

Example Question #1 : How To Multiply Rational Expressions

what is 6/8 X 20/3

Possible Answers:

9/40

18/160

3/20

120/11

Correct answer: 5

Explanation:

6/8 X 20/3 first step is to reduce 6/8 -> 3/4 (Divide top and bottom by 2)

3/4 X 20/3 (cross-cancel the threes and the 20 reduces to 5 and the 4 reduces to 1)

1/1 X 5/1 = 5

Report an Error

Example Question #8 : Rational Expressions

Evaluate and simplify the following product:

$\frac{15x^2+4xy^3-3y}{x^2y^7}\times\frac{5y^4}{4x^3}$

Possible Answers:

$\frac{20x^2+9xy^3-2y}{4x^5y^3}$

$\frac{75x^2+20xy^3-15y}{4x^5y^3}$

$\frac{75x^6+20xy^1^2-15y^4}{4x^6y^3}$

$\frac{75x^2y^-^3+20x-15y}{4x^5}$

Correct answer:

$\frac{75x^2+20xy^3-15y}{4x^5y^3}$

Explanation:

The procedure for multplying together two rational expressions is the same as multiplying together any two fractions: find the product of the numerators and the product of the denominators separately, and then simplify the resulting quotient as far as possible, as shown:

$\frac{15x^2+4xy^3-3y}{x^2y^7}\times\frac{5y^4}{4x^3}$

$=\frac{(15x^2+4xy^3-3y)(5y^4)}{(x^2y^7)(4x^3)}$

$=\frac{75x^2y^4+20xy^7-15y^5}{4x^5y^7}$

$=\frac{75x^2+20xy^3-15y}{4x^5y^3}$

Report an Error

View SAT Mathematics Tutors

Troy
Certified Tutor

Rice University, Bachelor in Arts, Kinesiology.

View SAT Mathematics Tutors

Sarah
Certified Tutor

New York University, Bachelor of Fine Arts, Drama.

View SAT Mathematics Tutors

Joy
Certified Tutor

Boston University, Bachelor in Arts, Conservation Biology.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

SAT Courses & Classes in Houston, LSAT Courses & Classes in Miami, GMAT Courses & Classes in Los Angeles, GRE Courses & Classes in Houston, ACT Courses & Classes in Phoenix, ACT Courses & Classes in Washington DC, LSAT Courses & Classes in Denver, GRE Courses & Classes in Boston, Spanish Courses & Classes in Chicago, SSAT Courses & Classes in San Diego

Popular Test Prep

GMAT Test Prep in Houston, GRE Test Prep in New York City, ACT Test Prep in Los Angeles, SAT Test Prep in New York City, SAT Test Prep in Denver, SSAT Test Prep in Atlanta, MCAT Test Prep in Houston, ACT Test Prep in Phoenix, GMAT Test Prep in Atlanta, LSAT Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Expressions

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #31 : Expressions

Example Question #32 : Expressions

Example Question #1 : How To Evaluate Rational Expressions

Example Question #2 : How To Evaluate Rational Expressions

Example Question #3 : How To Evaluate Rational Expressions

Example Question #4 : How To Evaluate Rational Expressions

Example Question #13 : Expressions

Example Question #311 : Algebra

Example Question #1 : How To Multiply Rational Expressions

Example Question #8 : Rational Expressions

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: