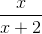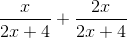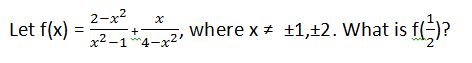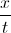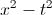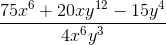To add rational expressions, first find the least common denominator. Because the denominator of the first fraction factors to 2(x+2), it is clear that this is the common denominator. Therefore, multiply the numerator and denominator of the second fraction by 2.

$\displaystyle \frac{x}{2x+4}+\frac{x}{x+2}$

$\displaystyle \frac{x}{2x+4}+\frac{(2)x}{(2)(x+2)}$

$\displaystyle \frac{x}{2x+4}+\frac{2x}{2x+4}$

$\displaystyle \frac{3x}{2x+4}$

This is the most simplified version of the rational expression.

To simplify the following, a common denominator must be achieved. In this case, the first term must be multiplied by (x+2) in both the numerator and denominator and likewise with the second term with (x-3).

$\displaystyle \frac{(x+3)(x+3)}{(x-2)(x+3)}+\frac{(x-2)(x-2)}{(x+3)(x-2)}$

$\displaystyle \frac{(x+3)^2+(x-2)^2}{(x+3)(x-2)}$

If we plug in a² for b in the radical expression, we get √(a³) = 8. This can be rewritten as a^3/2 = 8. Thus, log_a 8 = 3/2. Plugging in the answer choices gives 4 as the correct answer. 

To solve this, we need to set a proportion.

$\displaystyle \frac{100\:\text{ft}}{20\sec}=\frac{1500\:\text{ft}}{x}$

Cross Multiply

$\displaystyle 100\cdot x=1500\cdot 20$

$\displaystyle x=\frac{30000}{100}=300$

So it will take Jill $\displaystyle 300 \sec$ to walk $\displaystyle 1500\: \text{ft}$

$\displaystyle \frac{b+c}{c}=\frac{14}{15}$

$\displaystyle \frac{b}{c}+\frac{c}{c}=\frac{14}{15}$

$\displaystyle \frac{b}{c}+1=\frac{14}{15}$

$\displaystyle \frac{b}{c}+1\ {\color{Red} -1}=\frac{14}{15}\ {\color{Red} -1}$

$\displaystyle \frac{b}{c}=\frac{14}{15}-\frac{15}{15}$

$\displaystyle \frac{b}{c}=-\frac{1}{15}$

We will need to simplify the expression $\displaystyle \frac{(\frac{1}{t}-\frac{1}{x})}{x-t}$. We can think of this as a large fraction with a numerator of $\displaystyle \frac{1}{t}-\frac{1}{x}$ and a denominator of $\displaystyle \dpi{100} x-t$.

In order to simplify the numerator, we will need to combine the two fractions. When adding or subtracting fractions, we must have a common denominator. $\displaystyle \frac{1}{t}$ has a denominator of $\displaystyle \dpi{100} t$, and $\displaystyle \dpi{100} -\frac{1}{x}$ has a denominator of $\displaystyle \dpi{100} x$. The least common denominator that these two fractions have in common is $\displaystyle \dpi{100} xt$. Thus, we are going to write equivalent fractions with denominators of $\displaystyle \dpi{100} xt$.

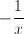
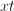
In order to convert the fraction $\displaystyle \dpi{100} \frac{1}{t}$ to a denominator with $\displaystyle \dpi{100} xt$, we will need to multiply the top and bottom by $\displaystyle \dpi{100} x$.

$\displaystyle \frac{1}{t}=\frac{1\cdot x}{t\cdot x}=\frac{x}{xt}$

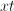
Similarly, we will multiply the top and bottom of $\displaystyle \dpi{100} -\frac{1}{x}$ by $\displaystyle \dpi{100} t$.

$\displaystyle \frac{1}{x}=\frac{1\cdot t}{x\cdot t}=\frac{t}{xt}$

We can now rewrite $\displaystyle \frac{1}{t}-\frac{1}{x}$ as follows:

$\displaystyle \frac{1}{t}-\frac{1}{x}$ = $\displaystyle \frac{x}{xt}-\frac{t}{xt}=\frac{x-t}{xt}$

Let's go back to the original fraction $\displaystyle \frac{(\frac{1}{t}-\frac{1}{x})}{x-t}$. We will now rewrite the numerator:

$\displaystyle \frac{(\frac{1}{t}-\frac{1}{x})}{x-t}$ = $\displaystyle \frac{\frac{x-t}{xt}}{x-t}$

To simplify this further, we can think of $\displaystyle \frac{\frac{x-t}{xt}}{x-t}$ as the same as $\displaystyle \frac{x-t}{xt}\div (x-t)$ . When we divide a fraction by another quantity, this is the same as multiplying the fraction by the reciprocal of that quantity. In other words, $\displaystyle a\div b=a\cdot \frac{1}{b}$.

$\displaystyle \frac{x-t}{xt}\div (x-t)$ = $\displaystyle \frac{x-t}{xt}\cdot \frac{1}{x-t}$$\displaystyle =\frac{x-t}{xt(x-t)}$$\displaystyle = \frac{1}{xt}$

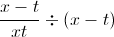
Lastly, we will use the property of exponents which states that, in general, $\displaystyle \frac{1}{a}=a^{-1}$.

$\displaystyle \frac{1}{xt}=(xt)^{-1}$

The answer is $\displaystyle (xt)^{-1}$.

Factor first.  The numerators will not factor, but the first denominator factors to (x – 2)(x + 2) and the second denomintaor factors to x(x – 2).  Multiplying fractions does not require common denominators, so now look for common factors to divide out.  There is a factor of x and a factor of (x + 2) that both divide out, leaving 4 in the numerator and two factors of (x – 2) in the denominator.

6/8 X 20/3 first step is to reduce 6/8 -> 3/4 (Divide top and bottom by 2)

3/4 X 20/3 (cross-cancel the threes and the 20 reduces to 5 and the 4 reduces to 1)

1/1 X 5/1 = 5

The procedure for multplying together two rational expressions is the same as multiplying together any two fractions: find the product of the numerators and the product of the denominators separately, and then simplify the resulting quotient as far as possible, as shown:

$\displaystyle \frac{15x^2+4xy^3-3y}{x^2y^7}\times\frac{5y^4}{4x^3}$

$\displaystyle =\frac{(15x^2+4xy^3-3y)(5y^4)}{(x^2y^7)(4x^3)}$

$\displaystyle =\frac{75x^2y^4+20xy^7-15y^5}{4x^5y^7}$

$\displaystyle =\frac{75x^2+20xy^3-15y}{4x^5y^3}$