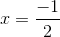To solve for \(\displaystyle x\), first convert both sides to the same base:

\(\displaystyle 5^{x} = \frac{1}{25}^{4x-1} = (5^{-2})^{4x-1} = 5^{-8x+2}\)

Now, with the same base, the exponents can be set equal to each other:

\(\displaystyle x= - 8x +2\)

Solving for \(\displaystyle x\) gives:

\(\displaystyle x = \frac{2}{9}\)

\(\displaystyle \log{_{4}}{x^{2}}+\log{_{4}}{3}=1\)

\(\displaystyle \Rightarrow \log{_{4}}{x^{2}}+\log{_{4}}{3}=\log{_{4}}{4}\)

\(\displaystyle \Rightarrow log{_{4}}{(x^{2}\times 3)}=\log{_{4}}{4}\)

\(\displaystyle \Rightarrow 3x^{2}=4\)

\(\displaystyle \Rightarrow x^{2}=\frac{4}{3}\)

\(\displaystyle \Rightarrow x=\frac{2\sqrt{3}}{3}, x=-\frac{2\sqrt{3}}{3}\)

Rewrite \(\displaystyle 24\) as a product that includes the number \(\displaystyle 3\):

\(\displaystyle \small \log_2 24 = \log_2 (2^3 \cdot 3)\)

Then we can split up the logarithm using the Product Property of Logarithms:

\(\displaystyle \small \log_2 (2^3\cdot 3) = \log_2 2^3 + \log_2 3\)

                     \(\displaystyle \small =3+\log_2 3\)

                     \(\displaystyle \small \approx 3 + 1.5850\)

Thus,

\(\displaystyle \small \log_2 24 \approx 4.5850\).

Rewrite in exponential form:

\(\displaystyle 9^{2}=2x+1\)

Solve for x:

\(\displaystyle 81=2x+1\)

\(\displaystyle x=40\)

For this problem it is helpful to remember that,

 \(\displaystyle ln(3x+8) = 0\) is equivalent to \(\displaystyle ln(3x+8) = ln(1)\) because \(\displaystyle ln(1)=0\)

Therefore we can set what is inside of the parentheses equal to each other and solve for \(\displaystyle x\) as follows:

\(\displaystyle 3x+8=1\)

\(\displaystyle 3x=-7\)

\(\displaystyle x=-\frac{7}{3}\)

To solve this logarithm, we need to know how to read a logarithm. A logarithm is the inverse of an exponential function. If a exponential equation is

\(\displaystyle a^c = b\)

then its inverse function, or logarithm, is

\(\displaystyle log_ab=c\)

Therefore, for this problem, in order to solve for \(\displaystyle x\), we simply need to solve

\(\displaystyle 6^5=x\)

which is \(\displaystyle 7776\).

Logs are exponential functions using base 10 and a property is that you can combine added logs by multiplying.

\(\displaystyle x(x+21)=10^{2}\)

\(\displaystyle x^{2}+21x=100\)

\(\displaystyle (x+25)(x-4)=0\)

You cannot take the log of a negative number.  x=-25  is extraneous.

This question is testing the definition of logs. \(\displaystyle \log_{a}b=x\) is the same as \(\displaystyle a^{x}=b\).

In this case, \(\displaystyle \log_{x}36=2\) can be rewritten as \(\displaystyle x^{2}=36\).

Taking square roots of both sides, you get \(\displaystyle x=\pm 6\). Since only the positive answer is one of the answer choices, \(\displaystyle 6\) is the correct answer.

The first step is to rewrite this equation in log form. 

When rewriting an exponential function as a log we must remember that the form of an exponential is: 

\(\displaystyle b^{^{x}}=a\)

When this is rewritten in log form it is: 

\(\displaystyle log{_{b}}(a)=x\).

Therefore we have \(\displaystyle 3^{x}=15\) which when rewritten gives us,

\(\displaystyle log{_{3}}{15}=x\).

Use the rule of Exponents of Logarithms to turn all the multipliers into exponents:

\(\displaystyle log_3x=log_364^\frac{1}{3}+log_349^\frac{1}{2}\).

Simplify by applying the exponents: \(\displaystyle log_3x=log_34+log_37\).

According to the law for adding logarithms, \(\displaystyle log_b(mn) = log_b(m) + log_b(n)\).

Therefore, multiply the 4 and 7.

\(\displaystyle log_3x=log_328\).

Because both sides have the same base, \(\displaystyle x=28\).