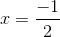Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Solving and Graphing Logarithms

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Solving Logarithmic Functions

Solve for :

$5^{x} = \left(\frac{1}{25}\right)^{4x-1}$

Possible Answers:

$x = \frac{1}{3}$

$x = \frac{1}{2}$

$x = \frac{2}{9}$

$x = \frac{-2}{7}$

$x = \frac{-1}{2}$

Correct answer:

$x = \frac{2}{9}$

Explanation:

To solve for , first convert both sides to the same base:

$5^{x} = \frac{1}{25}^{4x-1} = (5^{-2})^{4x-1} = 5^{-8x+2}$

Now, with the same base, the exponents can be set equal to each other:

x= - 8x +2

Solving for gives:

$x = \frac{2}{9}$

Report an Error

Example Question #2 : Solving Logarithms

Solve the equation:

$\log{_{4}}{x^{2}}+\log{_{4}}{3}=1$

Possible Answers:

$\frac{\sqrt{6}}{3}, -\frac{\sqrt{6}}{3}$

$\frac{\sqrt{3}}{3}, -\frac{\sqrt{3}}{3}$

$\frac{\sqrt{3}}{2}, -\frac{\sqrt{3}}{2}$

1,-1

$\frac{2\sqrt{3}}{3}, -\frac{2\sqrt{3}}{3}$

Correct answer:

$\frac{2\sqrt{3}}{3}, -\frac{2\sqrt{3}}{3}$

Explanation:

$\log{_{4}}{x^{2}}+\log{_{4}}{3}=1$

$\Rightarrow \log{_{4}}{x^{2}}+\log{_{4}}{3}=\log{_{4}}{4}$

$\Rightarrow log{_{4}}{(x^{2}\times 3)}=\log{_{4}}{4}$

$\Rightarrow 3x^{2}=4$

$\Rightarrow x^{2}=\frac{4}{3}$

$\Rightarrow x=\frac{2\sqrt{3}}{3}, x=-\frac{2\sqrt{3}}{3}$

Report an Error

Example Question #3 : Solving Logarithms

Use $\small \small \log_23\approx 1.5850$ to approximate the value of $\small \log_2 24$ .

Possible Answers:

$\small \log_2 24\approx 3.4150$

$\small \log_2 24\approx 12.5850$

$\small \log_2 24\approx 3.5850$

$\small \log_2 24\approx 4.5850$

$\small \log_2 24\approx 12.6800$

Correct answer:

$\small \log_2 24\approx 4.5850$

Explanation:

Rewrite as a product that includes the number :

$\small \log_2 24 = \log_2 (2^3 \cdot 3)$

Then we can split up the logarithm using the Product Property of Logarithms:

$\small \log_2 (2^3\cdot 3) = \log_2 2^3 + \log_2 3$

$\small =3+\log_2 3$

$\small \approx 3 + 1.5850$

Thus,

$\small \log_2 24 \approx 4.5850$ .

Report an Error

Example Question #3 : Solving Logarithms

Solve for .

$log_{9}^{ }(2x+1)=2$

Possible Answers:

x=40

$x=\frac{17}{2}$

$x=\frac{81}{2}$

x=20

x=41

Correct answer:

x=40

Explanation:

Rewrite in exponential form:

$9^{2}=2x+1$

Solve for x:

81=2x+1

x=40

Report an Error

Example Question #4 : Solving Logarithms

Solve the following equation:

ln(3x+8)=0

Possible Answers:

$-\frac{8}{3}$

$\frac{8}{7}$

$-\frac{7}{3}$

$\frac{1}{3}$

Correct answer:

$-\frac{7}{3}$

Explanation:

For this problem it is helpful to remember that,

ln(3x+8) = 0 is equivalent to ln(3x+8) = ln(1) because ln(1)=0

Therefore we can set what is inside of the parentheses equal to each other and solve for as follows:

3x+8=1

3x=-7

$x=-\frac{7}{3}$

Report an Error

Example Question #5 : Solving Logarithms

Solve for :

log_6x=5

Possible Answers:

15625

7776

10000

Correct answer:

7776

Explanation:

To solve this logarithm, we need to know how to read a logarithm. A logarithm is the inverse of an exponential function. If a exponential equation is

a^c = b

then its inverse function, or logarithm, is

log_ab=c

Therefore, for this problem, in order to solve for , we simply need to solve

6^5=x

which is 7776 .

Report an Error

Example Question #7 : Solving Logarithms

$\log x+\log\left ( x+21\right )=2$

Solve for .

Possible Answers:

100

Correct answer:

Explanation:

Logs are exponential functions using base 10 and a property is that you can combine added logs by multiplying.

$x(x+21)=10^{2}$

$x^{2}+21x=100$

(x+25)(x-4)=0

You cannot take the log of a negative number. x=-25 is extraneous.

Report an Error

Example Question #1 : Solving Logarithms

If $\log_{x}36=2$ , which of the following is a possible value for ?

Possible Answers:

Correct answer:

Explanation:

This question is testing the definition of logs. $\log_{a}b=x$ is the same as $a^{x}=b$ .

In this case, $\log_{x}36=2$ can be rewritten as $x^{2}=36$ .

Taking square roots of both sides, you get $x=\pm 6$ . Since only the positive answer is one of the answer choices, is the correct answer.

Report an Error

Example Question #9 : Solving Logarithms

Rewriting Logarithms in Exponential Form

Solve for below:

$3^{x}=15$

Which of the below represents this function in log form?

Possible Answers:

$log{_{x}}{3}=15$

$log{_{3}}{15}=x$

$log{_{x}}{15}=3$

$log{_{15}}{3}=x$

Correct answer:

$log{_{3}}{15}=x$

Explanation:

The first step is to rewrite this equation in log form.

When rewriting an exponential function as a log we must remember that the form of an exponential is:

$b^{^{x}}=a$

When this is rewritten in log form it is:

$log{_{b}}(a)=x$ .

Therefore we have $3^{x}=15$ which when rewritten gives us,

$log{_{3}}{15}=x$ .

Report an Error

Example Question #10 : Solving Logarithms

Solve for :

$log_3x=\frac{1}{3}log_364+\frac{1}{2}log_349$ .

Possible Answers:

Not enough information

x=45.8

x=28

x=11

x=522.7

Correct answer:

x=28

Explanation:

Use the rule of Exponents of Logarithms to turn all the multipliers into exponents:

$log_3x=log_364^\frac{1}{3}+log_349^\frac{1}{2}$ .

Simplify by applying the exponents: log_3x=log_34+log_37 .

According to the law for adding logarithms, log_b(mn) = log_b(m) + log_b(n) .

Therefore, multiply the 4 and 7.

log_3x=log_328 .

Because both sides have the same base, x=28 .

Report an Error

View Algebra 2 Tutors

Renetta
Certified Tutor

Langston University, Bachelor of Science, Education of Individuals in Elementary Special Education Programs.

View Algebra 2 Tutors

Michael
Certified Tutor

Kennesaw State University, Bachelor of Science, Mathematics.

View Algebra 2 Tutors

Brandon
Certified Tutor

Flager College, Bachelor, Elementary Education .

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Seattle, ISEE Tutors in Houston, Reading Tutors in New York City, Calculus Tutors in Dallas Fort Worth, SSAT Tutors in Boston, ACT Tutors in Chicago, GMAT Tutors in New York City, SSAT Tutors in Houston, Biology Tutors in Miami, LSAT Tutors in Seattle

Popular Courses & Classes

GRE Courses & Classes in Philadelphia, SAT Courses & Classes in Dallas Fort Worth, ACT Courses & Classes in Chicago, GMAT Courses & Classes in Los Angeles, ISEE Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in New York City, ISEE Courses & Classes in Los Angeles, SSAT Courses & Classes in Phoenix, GRE Courses & Classes in San Francisco-Bay Area, GMAT Courses & Classes in Phoenix

Popular Test Prep

ISEE Test Prep in Los Angeles, MCAT Test Prep in Chicago, MCAT Test Prep in Washington DC, ACT Test Prep in San Diego, GRE Test Prep in Los Angeles, SAT Test Prep in Seattle, GMAT Test Prep in Dallas Fort Worth, GMAT Test Prep in Miami, SAT Test Prep in Philadelphia, GMAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Solving and Graphing Logarithms

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #1 : Solving Logarithmic Functions

Example Question #2 : Solving Logarithms

Example Question #3 : Solving Logarithms

Example Question #3 : Solving Logarithms

Example Question #4 : Solving Logarithms

Example Question #5 : Solving Logarithms

Example Question #7 : Solving Logarithms

Example Question #1 : Solving Logarithms

Example Question #9 : Solving Logarithms

Example Question #10 : Solving Logarithms

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: